A 2 b 2 c 2 формула: Square of a Trinomial | (a + b + c)^2 Formula – Формулы сокращённого умножения

A 2 b 2 c 2, сложение квадратов

Выражения, преобразование выражений

Формулы сокращенного умножения (ФСУ): таблица, формулировки, примеры применения.

Для умножения и возведения в степень чисел и выражений (в частности многочленов) в некоторых случаях могут быть использованы так называемые формулы сокращенного умножения. Из названия понятно, что эти формулы позволяют проводить умножение сокращенно, то есть, быстрее при более компактной записи решения.

В этой статье мы перечислим все основные наиболее часто используемые формулы сокращенного умножения. Для удобства запоминания занесем их в таблицу. Дальше дадим формулировки – они позволят читать формулы сокращенного умножения. После этого остановимся на принципах доказательства этих формул. Наконец, дадим обзор задач, для решения которых применяются формулы сокращенного умножения, и рассмотрим несколько примеров с подробными решениями.

Список формул сокращенного умножения (ФСУ) в виде таблицы

Формулы сокращенного умножения (фсу) изучаются на уроках алгебры в 7 классе после разговора про действия с многочленами и одночленами, при этом рассматриваются 7 основных формул. Перечислим их по порядку в виде списка:

• (a+b)²=a²+2·a·b+b² – так называемая формула квадрата суммы;
• (a−b)²=a²−2·a·b+b² – эта формула имеет название квадрат разности;
• (a+b)³=a³+3·a²·b+3·a·b²+b³ – эта формула представляет собой куб суммы;
• (a−b)³=a³−3·a²·b+3·a·b²−b³ – формула куба разности;
• (a−b)·(a+b)=a²−b²;
• (a+b)·(a^2−a·b+b^2)=a^3+b^3;
• (a−b)·(a²+a·b+b²)=a³−b³.

Под буквами a и b понимаются числа, переменные, или, вообще, любые числовые и буквенные выражения.

Формулы сокращенного выражения очень часто применяются на практике, так что их все желательно выучить наизусть. До этого момента нам будет служить верой и правдой таблица формул сокращенного умножения, которую мы рекомендуем распечатать и все время держать перед глазами:

Первые четыре формулы из составленной таблицы формул сокращенного умножения позволяют возводить в квадрат и куб сумму или разность двух выражений. Пятая предназначена для краткого умножения разности и суммы двух выражений. А шестая и седьмая формулы используются для умножения суммы двух выражений a и b на их неполный квадрат разности (так называют выражение вида a²−a·b+b²) и разности двух выражений a и b на неполный квадрат их суммы (a²+a·b+b²) соответственно.

Стоит отдельно заметить, что каждое равенство в таблице представляет собой тождество. Этим объясняется, почему формулы сокращенного умножения еще называют тождествами сокращенного умножения.

При решении примеров, особенно в которых имеет место разложение многочлена на множители, ФСУ часто используют в виде с переставленными местами левыми и правыми частями:

Три последних тождества в таблице имеют свои названия.

Формула a²−b²=(a−b)·(a+b) называется формулой разности квадратов, a³+b³=(a+b)·(a²−a·b+b²) — формулой суммы кубов, а a³−b³=(a−b)·(a²+a·b+b²) — формулой разности кубов. Обратите внимание, что соответствующим формулам с переставленными частями из предыдущей таблицы фсу мы никак не назвали.

К началу страницы

Дополнительные формулы

В таблицу формул сокращенного умножения не помешает добавить еще несколько тождеств.

Во-первых, полезной будет формула бинома Ньютона вида , где — биномиальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. С ее помощью можно сокращенно возводить сумму двух выражений в любую натуральную степень. Кстати, ФСУ квадрата и куба суммы и разности являются частными случаями формулы бинома Ньютона при n=2 и n=3.

Во-вторых, полезной бывает формула возведения в квадрат суммы трех, четырех и большего количества слагаемых вида
(a₁+a₂+…+a_n)²=a₁²+a₂²+…+a_n−1²+a_n²

+
+2·a₁·a₂+2·a₁·a₃+2·a₁·a₄+…+
+2·a₁·a_n−1+2·a₁·a_n+
+2·a₂·a₃+2·a₂·a₄+…+2·a₂·a_n−1+2·a₂·a_n+
+…+
+2·a_n−1·a_n.

Она читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых. Для примера возведем в квадрат с использованием этой формулы сумму трех слагаемых a, b и c, имеем (a+b+c)²=a²+b²+c²+2·a·b+2·a·c+2·b·c. В частном случае при n=2 эта формула становится уже известной нам формулой квадрата суммы двух слагаемых.

И еще не помешает держать перед глазами формулу разности n-ых степеней двух слагаемых вида aⁿ−bⁿ=
=(a−b)·(aⁿ⁻¹+aⁿ⁻²·b+aⁿ⁻³·b²+…+a·b

n−2+bⁿ⁻¹), которую обычно представляют раздельно для четных и нечетных показателей. Для четных показателей 2·m она имеет вид a^2·m−b^2·m=
=(a²−b²)·(a^2·m−2+a^2·m−4·b²+a^2·m−6·b⁴+…+b^2·m−2), а для нечетных показателей 2·m+1 – вид a^2·m+1−b^2·m+1=
=(a−b)·(a^2·m+a^2·m−1·b+a^2·m−2·b²+…+b^2·m).

Частными случаями этой формулы являются формулы разность квадратов (при n=2), разность кубов (при n=3) и сумма кубов (при n=3 и если b заменить на −b).

К началу страницы

Как читаются формулы сокращенного умножения?

Чтобы рассказать решение примера, в котором были использованы формулы сокращенного умножения, нужно знать, как эти формулы читаются. Дадим соответствующие формулировки.

Сначала разберемся с принципом чтения формул сокращенного умножения. Это удобнее всего сделать, рассмотрев любую и них, например, первую формулу квадрата суммы вида (a+b)

2=a²+2·a·b+b².

В левой ее части находится выражение (a+b)², которое представляет собой квадрат суммы двух выражений a и b, оно так и читается (отсюда понятно и название формулы). Дальше стоит знак равно, он и произносится как равно. В правой части формулы расположена сумма трех слагаемых a², 2·a·b и b². a² и b² – это квадраты первого и второго выражений соответственно, а 2·a·b читается как удвоенное произведение выражений a и b, слово «удвоенное» отвечает числовому коэффициенту2. Осталось соединить все эти рассуждения в одно предложение, которое будет ответом на вопрос, как читается формула квадрата суммы.

Итак, квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения первого и второго выражений и квадрата второго выражения.

Аналогично читаются и остальные фсу.

Так квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение этих выражений плюс квадрат второго выражения. Эта формулировка второй фсу вида (a−b)

2=a²−2·a·b+b².

Дальше читаем формулу (a+b)³=a³+3·a²·b+3·a·b²+b³. Куб суммы двух выражений a и b равен сумме куба первого выражения, утроенного произведения квадрата первого выражения на второе, утроенного произведения первого выражения на квадрат второго и куба второго выражения.

Аналогично читается и формула куба разности (a−b)³=a³−3·a²·b+3·a·b²−b³. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого на квадрат второго выражения минус куб второго выражения.

Переходим к чтению пятой по списку формулы сокращенного выражения (a−b)·(a+b)=a

2−b². Произведение разности двух выражений и их суммы равно разности квадратов первого и второго выражений.

А для удобства чтения шестой и, последней, седьмой ФСУ используют термины «неполный квадрат суммы» и «неполный квадрат разности» выражений a и b, которыми называют выражения a²+a·b+b² и a²−a·b+b² соответственно. (В свою очередь выражения a²+2·a·b+b² и a²−2·a·b+b² называют полным квадратом суммы и разности соответственно.)

Итак, произведение суммы двух выражений на их неполный квадрат разности равно сумме кубов этих выражений.

Теорема косинусов. Доказательство теоремы косинусов.

Так читается формула (a+b)·(a²−a·b+b²)=a³+b³. И произведение разности двух выражений на неполный квадрат их суммы равен разности кубов этих выражений, этому утверждению отвечает формула сокращенного умножения вида (a−b)·(a²+a·b+b²)=a³

−b³.

К началу страницы

Доказательство

Сейчас самое время остановиться на доказательстве формул сокращенного умножения.

Доказать их достаточно легко – для этого нужно лишь выполнить возведение в степень или умножение выражений, находящихся в левых частях формул, основываясь на свойствах умножения.

Для примера докажем формулу квадрата разности (a−b)²=a²−2·a·b+b². Возведем разность a−b во вторую степень. Для этого степень заменяем умножением, и выполняем это действие: (a−b)²=(a−b)·(a−b)=
=a·(a−b)−b·(a−b)=a·a+a·(−b)−b·a−b·(−b)=
=a²−a·b−b·a+b·b=a²−a·b−a·b+b²=
=a²−2·a·b+b².

Абсолютно аналогично доказывается любая другая из 7 основных формул сокращенного умножения.

Доказательство дополнительных ФСУ можно провести с использованием метода наименьших квадратов.

К началу страницы

Сферы применения формул сокращенного умножения (фсу) и примеры

Основное предназначение формул сокращенного умножения (фсу) объясняется их названием, то есть, оно состоит в кратком умножении выражений. Однако сфера применения ФСУ намного шире, и не ограничивается кратким умножением. Перечислим основные направления.

Несомненно, центральное приложение формулы сокращенного умножения нашли в выполнении тождественных преобразований выражений. Наиболее часто эти формулы используются в процессе упрощения выражений.

Упростите выражение 9·y−(1+3·y)².

В данном выражении возведение в квадрат можно выполнить сокращенно, имеем 9·y−(1+3·y)²=9·y−(1²+2·1·3·y+(3·y)²). Остается лишь раскрыть скобки и привести подобные члены: 9·y−(1²+2·1·3·y+(3·y)²)=9·y−1−6·y−9·y²=3·y−1−9·y².

9·y−(1+3·y)²=3·y−1−9·y².

И если в 7 классе речь идет о преобразовании целых выражений с помощью формул сокращенного умножения, то в старших классах можно будет видеть применение ФСУ к преобразованию выражений всех других видов – дробных, иррациональных, логарифмических, тригонометрических и других. К примеру, тождества сокращенного умножения с переставленными частями позволяют представлять выражения в виде степеней или произведений, в частности, выполнять разложение многочленов на множители. Это очень полезно, к примеру, при сокращении алгебраических дробей.

Формулы сокращенного умножения иногда позволяют рационально вычислять значения выражений. В качестве примера покажем, как можно возвести число 79 в квадрат с помощью формулы квадрата разности: 79²=(80−1)²=80²−2·80·1+1²=6 400−160+1=6 241. Такой подход позволяет выполнять подобные вычисления даже устно.

В заключение скажем еще про одно важное преобразование – выделение квадрата двучлена, в основе которого лежит формула сокращенного умножения квадрат суммы. Например, выражение 4·x²+4·x−3 может быть преобразовано к виду (2·x)

2+2·2·x·1+1²−4, и первые три слагаемых заменяются с использованием формулы квадратом суммы. Так что выражение принимает вид (2·x+1)²−4. Подобные преобразования широко используются, например, при интегрировании.

Профиль автора статьи в Google+

К началу страницы

• Алгебра: учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 17-е изд. — М. : Просвещение, 2008. — 240 с. : ил. — ISBN 978-5-09-019315-3.
• Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 13-е изд., испр. — М.: Мнемозина, 2009. — 160 с.: ил. ISBN 978-5-346-01198-9.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Формулы сокращенного умножения с примерами

Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.

ФСУ используются при упрощении алгебраических выражений (в том числе в работе с алгебраическими дробями), решении уравнений и неравенств, при разложении на множители и т.д. Ниже мы рассмотрим наиболее популярные формулы и разберем как они получаются.

Квадрат суммы

Пусть у нас возводиться в квадрат сумма двух одночленов, вот так: \((a+b)^2\). Возведение в квадрат – это умножение числа или выражения само на себя, то есть, \((a+b)^2=(a+b)(a+b)\). Теперь мы можем просто раскрыть скобки, перемножив их как делали это здесь, и привести подобные слагаемые. Получаем:

А если мы опустим промежуточные вычисления и запишем только начальное и конечное выражения, получим окончательную формулу:

Квадрат суммы: \((a+b)^2=a^2+2ab+b^2\)

Большинство учеников учат ее наизусть. А вы теперь знаете, как эту формулу вывести, и если вдруг забудете – всегда можете это сделать.

Хорошо, но как ей пользоваться и зачем эта формула нужна? Квадрат суммы позволяет быстро писать результат возведения суммы двух слагаемых в квадрат. Давайте посмотрим на примере.

Пример. Раскрыть скобки: \((x+5)^2\)
Решение:

Обратите внимание, насколько быстрее и меньшими усилиями получен результат во втором случае. А когда вы эту и другие формулы освоите до автоматизма – будет еще быстрее: вы сможете просто сразу же писать ответ. Поэтому они и называются формулы СОКРАЩЕННОГО умножения. Так что, знать их и научиться применять – точно стоит.

На всякий случай отметим, что в качестве \(a\) и \(b\) могут быть любые выражения – принцип остается тем же. Например:

Если вы вдруг не поняли какие-то преобразования в двух последних примерах – повторите свойства степеней и тему приведения одночлена к стандартному виду.

Пример. Преобразуйте выражение \((1+5x)^2-12x-1 \) в многочлен стандартного вида.

Решение:

\((1+5x)^2-12x-1= \)		Раскроем скобки, воспользовавшись формулой квадрата суммы…
\(=1+10x+25x^2-12x-1=\)		…и приведем подобные слагаемые.
\(=25x^2-2x\)		Готово.

Ответ: \(25x^2-2x\).

Важно! Необходимо научиться пользоваться формулами не только в «прямом», но и в «обратном» направлении.

Пример. Вычислите значение выражения \((368)^2+2·368·132+(132)^2\) без калькулятора.

Решение:

\((368)^2+2·368·132+(132)^2=\)		Мда… возводить в квадрат трехзначные числа, перемножить их же, а потом все это складывать – удовольствие ниже среднего. Давайте искать другой путь: обратите внимание, что данное нам числовое выражение очень похоже на правую часть формулы. Применим ее в обратную сторону: \(a^2+2ab+b^2=(a+b)^2\)
\(=(368+132)^2=\)		Вот теперь вычислять гораздо приятнее!
\(=(500)^2=250 000.\)		Готово.

Ответ: \(250 000\).

Квадрат разности

Выше мы нашли формулу для суммы одночленов. Давайте теперь найдем формулу для разности, то есть, для \((a-b)^2\):

В более краткой записи имеем:

Квадрат разности: \((a-b)^2=a^2-2ab+b^2\)

Применяется она также, как и предыдущая.

Пример. Упростите выражение \((2a-3)^2-4(a^2-a)\) и найдите его значение при \(a=\frac{17}{8}\).

Решение:

\((2a-3)^2-4(a^2-a)=\)		Если сразу подставить дробь в выражение – придется возводить ее в квадрат и вообще делать объемные вычисления. Попробуем сначала упростить выражение, воспользовавшись формулой выше и раскрыв скобки.
\(=4a^2-12a+9-4a^2+4a=\)		Теперь приведем подобные слагаемые.
\(=-8a+9=\)		Вот теперь подставляем и наслаждаемся простотой вычислений.
\(=-8·\frac{17}{8}+9=-17+9=8\)		Пишем ответ.

Ответ: \(8\).

Разность квадратов

Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:

Получили формулу:

Разность квадратов \(a^2-b^2=(a+b)(a-b)\)

Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями. 

Пример. Сократите дробь \(\frac{x^2-9}{x-3}\).

Решение:

\(\frac{x^2-9}{x-3}\)\(=\)		Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус! Попробуем воспользоваться формулой.
\(=\) \(\frac{x^2-3^2}{x-3}\)\(=\)\(\frac{(x+3)(x-3)}{x-3}\)\(=\)		Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки.
\(=x+3\)		Готов ответ.

Ответ: \(x+3\).

Пример.Разложите на множители \(25x^4-m^{10} t^6\).
Решение:

\(25x^4-m^{10} t^6\)		Воспользуемся формулами степеней: \((a^n )^m=a^{nm}\) и \(a^n b^n=(ab)^n\).
\(=(5x^2 )^2-(m^5 t^3 )^2=\)		Ну, а теперь пользуемся формулой \(a^2-b^2=(a+b)(a-b)\), где \(a=5x^2\) и \(b=m^5 t^3\).
\(=(5x^2-m^5 t^3 )(5x^2+m^5 t^3 )\)		Готов ответ.

Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.

Пример (повышенной сложности!).Сократите дробь \(\frac{x^2-4xy-9+4y^2}{x-2y+3}\) .
Решение:

\(\frac{x^2-4xy-9+4y^2}{x-2y+3}\)\(=\)		На первый взгляд тут тихий ужас и сделать с ним ничего нельзя (вариант «лечь и помереть» всерьез не рассматриваем). Однако давайте попробуем поменять два последних слагаемых числителя местами и добавим скобки (просто для наглядности).
\(\frac{(x^2-4xy+4y^2)-9}{x-2y+3}\)\(=\)		Теперь немного преобразуем слагаемые в скобке: \(4xy\) запишем как \(2·x·2y\), а \(4y^2\) как \((2y)^2\).
\(\frac{(x^2-4xy+(2y)^2)-9}{x-2y+3}\)\(=\)		Теперь приглядимся – и заметим, что в скобке у нас получилась формула квадрата разности, у которой \(a=x\), \(b=2y\). Сворачиваем по ней к виду скобки в квадрате. И одновременно представляем девятку как \(3\) в квадрате.
\(\frac{(x-2y)^2-3^2}{x-2y+3}\)\(=\)		Еще раз внимательно смотрим на числитель… думаем… думаем… и замечаем формулу разности квадратов, у которой \(a=(x-2y)\), \(b=3\). Раскладываем по ней к произведению двух скобок.
\(\frac{(x-2y-3)(x-2y+3)}{x-2y+3}\)\(=\)		И вот теперь сокращаем вторую скобку числителя и весь знаменатель.
\(x-2y-3\)		Готов ответ.

Скачать статью

7.3.1. Примеры для закрепления формул сокращенного умножения

1)    Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

       (a+b)² = a²+2ab+b² 

  a) (x + 2y)² = x² + 2 ·x·2y + (2y)² = x² + 4xy + 4y²

б) (2k + 3n)² = (2k)² + 2·2k·3n + (3n)² = 4k² + 12kn + 9n²

2)    Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

        (a-b)² = a²-2ab+b²

 а)   (2a – c)² = (2a)²-2·2a·c + c² = 4a² – 4ac + c²

б)   (3a – 5b)² = (3a)²-2·3a·5b + (5b)² = 9a² – 30ab + 25b²

3)    Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.

         a²–b² = (a–b)(a+b)

a)      9x² – 16y² = (3x)² – (4y)² = (3x – 4y)(3x + 4y)

б)  (6k – 5n)( 6k + 5n) = (6k)² – (5n)² = 36k² – 25n²

4)  Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

        (a+b)³ = a³+3a²b+3ab²+b³

a)  (m + 2n)³ = m³ + 3·m²·2n + 3·m·(2n)² + (2n)³ = m³ + 6m²n + 12mn² + 8n³

б)  (3x + 2y)³ = (3x)³ + 3·(3x)²·2y + 3·3x·(2y)² + (2y)³ = 27x³ + 54x²y + 36xy² + 8y³

5)  Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a-b)³ = a³-3a²b+3ab²-b³

а)  (2x – y)³ = (2x)³-3·(2x)²·y + 3·2x·y² – y³ = 8x³ – 12x²y + 6xy² – y³

б)  (x – 3n)³ = x³-3·x²·3n + 3·x·(3n)² – (3n)³ = x³ – 9x²n + 27xn² – 27n³

6)  Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.

a³+b³ = (a+b)(a²–ab+b²)

a)      125 + 8x³ = 5³ + (2x)³ = (5 + 2x)(5² — 5·2x + (2x)²) = (5 + 2x)(25 – 10x + 4x²)

б)  (1 + 3m)(1 – 3m + 9m²) = 1³ + (3m)³ = 1 + 27m³

7)  Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.

 a³-b³ = (a-b)(a²+ab+b²)

а) 64с³ – 8 = (4с)³ – 2³ = (4с – 2)((4с)² + 4с·2 + 2²) = (4с – 2)(16с² + 8с + 4)

б) (3a – 5b)(9a² + 15ab + 25b²) = (3a)³ – (5b)³ = 27a³ – 125b³

Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.

 

Запись имеет метки: Правила и формулы сокращенного умножения

Формулы сокращенного умножения.

Формулы сокращенного умножения.

Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.

Разность квадратов	a2-b2 = (a-b)(a+b)
Квадрат суммы	(a+b)2 = a2+2ab+b2
Квадрат разности	(a-b)2 = a2-2ab+b2
Куб суммы	(a+b)3 = a3+3a2b+3ab2+b3
Куб разности	(a-b)3 = a3-3a2b+3ab2-b3
Сумма кубов	a3+b3 = (a+b)(a2-ab+b2)
Разность кубов	a3-b3 = (a-b)(a2+ab+b2)
Разность четвертых степеней	a4-b4 = (a2-b2)(a2+b2)=(a-b)(a+b)(a2+b2)

Справочно, только для тех кто хочет больше представлять тему: Бином Ньютона. Целая положительная степень n суммы. (a + b)ⁿ=

Формулы сокращенного умножения

Формулы сокращенного умножения

Номер	Название формулы	Короткая запись	Раскрытие скобок/разложение на множители
(1)	Разность квадратов	a2-b2	(a-b)(a+b)
(2)	Квадрат суммы/разности	(a±b)2	a2±2ab+b2
(3)	Квадрат суммы для n переменных	(a1+a2+…+an)2	a12+a22+…+an2+2∑i,jaiaj
(4)	Сумма/разность кубов	a3±b3	(a±b)(a2∓ab+b2)
(5)	Куб суммы/разности	(a±b)3	a3±3a2b+3ab2±b3
(6)	Куб суммы для n переменных	(a1+a2+…+an)3	a13+a23+…+an3+3∑i,jai2aj+6∑i,j,kaiajak
(7)	Разность четвертых степеней	a4-b4	(a-b)(a+b)(a2+b2)
(8)	Четвертая степень суммы/разности	(a±b)4	a4±4a3b+6a2b2±4ab3+b4
(9)	Сумма/разность nх степеней	an-bn	(a±b)(an-1+an-2b+an-3b2+…+bn-3a2+bn-2a+bn-1)
(10)	Сумма (2n+1)х степеней	a2n+1+b2n+1	(a+b)(a2n-a2n-1b+a2n-2b2+…+b2n-2a2-b2n-1a+b2n)
(11)	Nая степень суммы/разности	(a±b)n	an±(n1)an-1b+(n2)an-2b2±..+(nn-2)a2bn-2±(nn-1)abn-1+bn

— версия для печати

---

Определение

N^ая степень числа — результат умножения числа на себя n раз. Также квадратом числа называется результат возведения числа в степень n (в n^ую степень).

Пример:

(4a—3b)³ = 64a³ — 144a²b + 108ab² — 27b³

Пояснение

Под (ⁿ_k) подразумевается биномиальный коэффициент, равный

Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью.

© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016

Квадратное уравнение — Википедия

Квадра́тное уравне́ние — алгебраическое уравнение общего вида

ax2+bx+c=0,{\displaystyle ax^{2}+bx+c=0,}

где x{\displaystyle x} — неизвестное, a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c} — коэффициенты, причём a≠0.{\displaystyle \quad a\neq 0.}

Выражение ax2+bx+c{\displaystyle ax^{2}+bx+c} называют квадратным трёхчленом^[1].

Корень — это значение переменной x{\displaystyle x}, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное числовое равенство.

Элементы квадратного уравнения имеют собственные названия^[1]:

• a{\displaystyle a} называют первым или старшим коэффициентом,
• b{\displaystyle b} называют вторым, средним или коэффициентом при x{\displaystyle x},
• c{\displaystyle c} называют свободным членом.

Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице^[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент a{\displaystyle a}:

x2+px+q=0,p=ba,q=ca.{\displaystyle x^{2}+px+q=0,\quad p={\frac {b}{a}},\quad q={\frac {c}{a}}.}

Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.

Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.

Исторические сведения о квадратных уравнениях[править | править код]

Древний Вавилон[править | править код]

Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения^[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:

x2+x=34; x2−x=1412.{\displaystyle x^{2}+x={\frac {3}{4}};\ x^{2}-x=14{\frac {1}{2}}.}

Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.

Индия[править | править код]

Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)^[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: ax2+bx=c{\displaystyle ax^{2}+bx=c}; притом предполагалось, что в нём все коэффициенты, кроме a,{\displaystyle a,} могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.

I способ. Общая формула для вычисления корней[править | править код]

Для нахождения корней квадратного уравнения ax2+bx+c=0{\displaystyle ax^{2}+bx+c=0} в общем случае следует пользоваться приводимым ниже алгоритмом:

Выведение формулы

Формулу можно получить следующим образом:

ax2+bx+c=0,{\displaystyle ax^{2}+bx+c=0,}

ax2+bx=−c{\displaystyle ax^{2}+bx=-c}

Умножаем каждую часть на 4a{\displaystyle 4a} и прибавляем b2{\displaystyle b^{2}}:

4a2x2+4abx+b2=−4ac+b2{\displaystyle 4a^{2}x^{2}+4abx+b^{2}=-4ac+b^{2}}

(2ax+b)2=−4ac+b2{\displaystyle (2ax+b)^{2}=-4ac+b^{2}}

2ax+b=±−4ac+b2{\displaystyle 2ax+b=\pm {\sqrt {-4ac+b^{2}}}}

2ax=−b±−4ac+b2{\displaystyle 2ax=-b\pm {\sqrt {-4ac+b^{2}}}}

x1,2=−b±b2−4ac2a.{\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.}

Примечание: очевидно, что формула для корня кратности 2 является частным случаем общей формулы, получается при подстановке в неё равенства D=0, а вывод о отсутствии вещественных корней при D<0 следует также сделать, учтя, что в этом случае -D>0, а −1=i{\displaystyle {\sqrt {-1}}=i}.

Изложенный метод универсален, однако он далеко не единственный.

II способ. Корни квадратного уравнения при чётном коэффициенте b[править | править код]

Для уравнений вида ax2+2kx+c=0{\displaystyle ax^{2}+2kx+c=0}, то есть при чётном b{\displaystyle b}, где

k=12b,{\displaystyle k={\frac {1}{2}}b,}

вместо формулы (1) для нахождения корней можно использовать более простые выражения^[1].

Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b=2k и совершив при этом несложные преобразования.

III способ. Решение неполных квадратных уравнений[править | править код]

К решению неполных квадратных уравнений следует подходить по-особому. Рассмотрим три возможных ситуации.

IV способ. Использование частных соотношений коэффициентов[править | править код]

Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.

Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту[править | править код]

Если в квадратном уравнении ax2+bx+c=0{\displaystyle ax^{2}+bx+c=0} сумма первого коэффициента и свободного члена равна второму коэффициенту: a+c=b{\displaystyle a+c=b}, то его корнями являются −1{\displaystyle -1} и число, противоположное отношению свободного члена к старшему коэффициенту (−ca{\displaystyle -{\frac {c}{a}}}).

Доказательство

Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):

D=b2−4ac=(a+c)2−4ac=a2+2ac+c2−4ac=a2−2ac+c2=(a−c)2{\displaystyle D=b^{2}-4ac=(a+c)^{2}-4ac=a^{2}+2ac+c^{2}-4ac=a^{2}-2ac+c^{2}=(a-c)^{2}}.

Да, это так, ведь при любых действительных значениях коэффициентов (a−c)2⩾0{\displaystyle (a-c)^{2}\geqslant 0}, а значит и дискриминант неотрицателен. Таким образом, если a≠c{\displaystyle a\not =c}, то уравнение имеет два корня, если же a=c{\displaystyle a=c}, то оно имеет только один корень.
Найдём эти корни:

x1,2=−b±D2a=−(a+c)±(a−c)22a=−a−c±|a−c|2a=−a−c±a∓c2a{\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}={\frac {-(a+c)\pm {\sqrt {(a-c)^{2}}}}{2a}}={\frac {-a-c\pm |a-c|}{2a}}={\frac {-a-c\pm a\mp c}{2a}}}.

x1=−a−c−a+c2a=−2a2a=−1;{\displaystyle x_{1}={\frac {-a-c-a+c}{2a}}={\frac {-2a}{2a}}=-1;}

x2=−a−c+a−c2a=−2c2a=−ca.{\displaystyle x_{2}={\frac {-a-c+a-c}{2a}}={\frac {-2c}{2a}}=-{\frac {c}{a}}.}

В частности, если a=c{\displaystyle a=c}, то корень будет один: −1.{\displaystyle -1.}

Способ 2. Геометрическая интерпретация: парабола, заданная аналитически указанной формулой, пересекает ось x в двух точках, абсциссами которых и являются корни, хотя бы один из которых равен -1

Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы y=ax2+bx+c{\displaystyle y=ax^{2}+bx+c} с осью абсцисс. Всякая парабола вне зависимости от задающего её выражения является фигурой, симметричной относительно прямой x=−b2a{\displaystyle x=-{\frac {b}{2a}}}. Это означает, что отрезок всякой перпендикулярной к ней прямой, отсекаемый на ней параболой, делится осью симметрии пополам. Сказанное, в частности, верно и для оси абсцисс. Таким образом, для всякой параболы справедливо одно из следующих равенств: −b2a+ρ(x1;−b2a)=x2{\displaystyle -{\frac {b}{2a}}+\rho (x_{1};-{\frac {b}{2a}})=x_{2}} (если x1<x2{\displaystyle x_{1}<x_{2}}) или −b2a−ρ(−b2a;x1)=x2{\displaystyle -{\frac {b}{2a}}-\rho (-{\frac {b}{2a}};x_{1})=x_{2}} (если верно неравенство противоположного смысла). Используя тождество ρ(a;b)=|a−b|{\displaystyle \rho (a;b)=|a-b|}, выражающее геометрический смысл модуля, а также принимая, что x1=−1{\displaystyle x_{1}=-1} (это можно доказать, подставив равенство в квадратный трёхчлен: a⋅(−1)2+b⋅(−1)+c=(a+c)−b=0{\displaystyle a\cdot (-1)^{2}+b\cdot (-1)+c=(a+c)-b=0}, поэтому -1 — корень такого уравнения) , приходим к следующему равенству: −b2a±|−b2a−(−1)|=x2.{\displaystyle -{\frac {b}{2a}}\pm |-{\frac {b}{2a}}-(-1)|=x_{2}.} Если учитывать, что разность в том случае, когда мы прибавляем модуль, всегда положительна, а в том, когда отнимаем — отрицательна, что говорит о тождественности этих случаев, и, к тому же, помня о равенстве b−a=c{\displaystyle b-a=c}, раскрываем модуль: x2=−b2a−b2a+1=−2b−2a2a=−b−aa=−ca{\displaystyle x_{2}=-{\frac {b}{2a}}-{\frac {b}{2a}}+1=-{\frac {2b-2a}{2a}}=-{\frac {b-a}{a}}=-{\frac {c}{a}}}. Во втором случае,совершив аналогичные преобразования, придём к тому же результату, ч.т.д.

Отсюда, прежде, чем решать какое-либо квадратное уравнение, следует проверить возможность применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.

Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю[править | править код]

Если в квадратном уравнении сумма всех его коэффициентов равна нулю (a+b+c=0{\displaystyle a+b+c=0}), то корнями такого уравнения являются 1{\displaystyle 1} и отношение свободного члена к старшему коэффициенту (ca{\displaystyle {\frac {c}{a}}}).

Доказательство

Способ 1. Прежде всего заметим, что из равенства a+b+c=0{\displaystyle a+b+c=0} следует, что b=−(a+c){\displaystyle b=-(a+c)}
Установим количество корней:

D=b2−4ac=(−(a+c))2−4ac=a2+2ac+c2−4ac=a2−2ac+c2=(a−c)2.{\displaystyle D=b^{2}-4ac=(-(a+c))^{2}-4ac=a^{2}+2ac+c^{2}-4ac=a^{2}-2ac+c^{2}=(a-c)^{2}.}

При любых значениях коэффициентов уравнение имеет хотя бы один корень: действительно, ведь при любых значениях коэффициентов (a−c)2⩾0{\displaystyle (a-c)^{2}\geqslant 0}, а значит и дискриминант неотрицателен. Обратите внимание, что если a≠c{\displaystyle a\not =c}, то уравнение имеет два корня, если же a=c{\displaystyle a=c}, то только один.
Найдём эти корни:

x1,2=−b±D2a=a+c±(a−c)22a=a+c±|a−c|2a=a+c±a∓c2a;{\displaystyle x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}={\frac {a+c\pm {\sqrt {(a-c)^{2}}}}{2a}}={\frac {a+c\pm |a-c|}{2a}}={\frac {a+c\pm a\mp c}{2a}};}

x1=a+c+a−c2a=2a2a=1;{\displaystyle x_{1}={\frac {a+c+a-c}{2a}}={\frac {2a}{2a}}=1;}

x2=a+c−a+c2a=2c2a=ca,{\displaystyle x_{2}={\frac {a+c-a+c}{2a}}={\frac {2c}{2a}}={\frac {c}{a}},}

что и требовалось доказать.

В частности, если a=c{\displaystyle a=c}, то уравнение имеет только один корень, которым является число 1{\displaystyle 1}.

Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: a⋅12+b⋅1+c=0{\displaystyle a\cdot 1^{2}+b\cdot 1+c=0} — верное равенство, следовательно, единица — корень такого вида квадратных уравнений. Далее, по теореме Виета находим второй корень: согласно этой теореме, произведение корней уравнения равно числу, равному отношению свободного члена к старшему коэффициенту — x1x2=ca⇒x2=cax1=ca⋅1=ca{\displaystyle x_{1}x_{2}={\frac {c}{a}}\Rightarrow x_{2}={\frac {c}{ax_{1}}}={\frac {c}{a\cdot 1}}={\frac {c}{a}}}, ч.т.д.

Отсюда, прежде, чем решать уравнение стандартными методами, следует проверить применимость к нему этой теоремы: сложить все коэффициенты данного уравнения и посмотреть, не равна ли нулю эта сумма.

V способ. Разложение квадратного трёхчлена на линейные множители[править | править код]

Если трёхчлен вида ax2+bx+c(a≠0){\displaystyle ax^{2}+bx+c(a\not =0)} удастся каким-либо образом представить в качестве произведения линейных множителей (kx+m)(lx+n)=0{\displaystyle (kx+m)(lx+n)=0}, то можно найти корни уравнения ax2+bx+c=0{\displaystyle ax^{2}+bx+c=0} — ими будут −mk{\displaystyle -{\frac {m}{k}}} и −

Формула Герона — Википедия

Материал из Википедии — свободной энциклопедии

Фо́рмула Герона позволяет вычислить площадь треугольника S{\displaystyle S} по его сторонам a,b,c{\displaystyle a,b,c}:

S=p(p−a)(p−b)(p−c),{\displaystyle S={\sqrt {p(p-a)(p-b)(p-c)}},}

где p{\displaystyle p} — полупериметр треугольника: p=a+b+c2{\displaystyle p={\frac {a+b+c}{2}}}.

Доказательство 1 (тригонометрическое):

S=12ab⋅sin⁡γ{\displaystyle S={1 \over 2}ab\cdot \sin {\gamma }},

где  γ{\displaystyle \ \gamma } — угол треугольника, противолежащий стороне c{\displaystyle c}.
По теореме косинусов:

c2=a2+b2−2ab⋅cos⁡γ,{\displaystyle c^{2}=a^{2}+b^{2}-2ab\cdot \cos \gamma ,}

Отсюда:

cos⁡γ=a2+b2−c22ab,{\displaystyle \cos \gamma ={a^{2}+b^{2}-c^{2} \over 2ab},}

Значит,

 sin2⁡γ=1−cos2⁡γ=(1−cos⁡γ)(1+cos⁡γ)={\displaystyle \ \sin ^{2}\gamma =1-\cos ^{2}\gamma =(1-\cos \gamma )(1+\cos \gamma )=}

=2ab−a2−b2+c22ab⋅2ab+a2+b2−c22ab={\displaystyle ={{2ab-a^{2}-b^{2}+c^{2}} \over 2ab}\cdot {{2ab+a^{2}+b^{2}-c^{2}} \over 2ab}=}

=c2−(a−b)22ab⋅(a+b)2−c22ab=14a2b2(c−a+b)(c+a−b)(a+b−c)(a+b+c){\displaystyle ={{c^{2}-(a-b)^{2}} \over 2ab}\cdot {{(a+b)^{2}-c^{2}} \over 2ab}={1 \over 4a^{2}b^{2}}(c-a+b)(c+a-b)(a+b-c)(a+b+c)}.

Замечая, что a+b+c=2p{\displaystyle a+b+c=2p}, a+b−c=2p−2c{\displaystyle a+b-c=2p-2c}, a+c−b=2p−2b{\displaystyle a+c-b=2p-2b}, c−a+b=2p−2a{\displaystyle c-a+b=2p-2a}, получаем:

sin⁡γ=2abp(p−a)(p−b)(p−c).{\displaystyle \sin \gamma ={2 \over ab}{\sqrt {p(p-a)(p-b)(p-c)}}.}

Таким образом,

S=12absin⁡γ=p(p−a)(p−b)(p−c),{\displaystyle S={1 \over 2}ab\sin \gamma ={\sqrt {p(p-a)(p-b)(p-c)}},}

ч.т.д.

Доказательство 2 (на основе теоремы Пифагора):

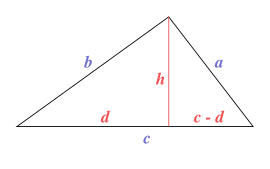Треугольник со сторонами a, b, c и высотой h, разделяющей основание c на d и (c − d).

По теореме Пифагора имеем следующие равенства для гипотенуз: a² = h² + (c − d)² и b² = h² + d² — см. рисунок справа. Вычитая из первого равенства второе, получаем a² − b² = c² − 2cd. Это уравнение позволяет нам выразить d через стороны треугольника:

d=−a2+b2+c22c{\displaystyle d={\frac {-a^{2}+b^{2}+c^{2}}{2c}}}

Для высоты h у нас было равенство h² = b² − d², в которое можно подставить полученное выражение для d и применить формулы для квадратов:

h3=b2−(−a2+b2+c22c)2=(2bc−a2+b2+c2)(2bc+a2−b2−c2)4c2=((b+c)2−a2)(a2−(b−c)2)4c2=(b+c−a)(b+c+a)(a+b−c)(a−b+c)4c2{\displaystyle {\begin{aligned}h^{2}&=b^{2}-\left({\frac {-a^{2}+b^{2}+c^{2}}{2c}}\right)^{2}={\frac {(2bc-a^{2}+b^{2}+c^{2})(2bc+a^{2}-b^{2}-c^{2})}{4c^{2}}}\\&={\frac {((b+c)^{2}-a^{2})(a^{2}-(b-c)^{2})}{4c^{2}}}={\frac {(b+c-a)(b+c+a)(a+b-c)(a-b+c)}{4c^{2}}}\\\end{aligned}}}

Замечая, что b+c−a=2p−2a{\displaystyle b+c-a=2p-2a}, a+b+c=2p{\displaystyle a+b+c=2p}, a+b−c=2p−2c{\displaystyle a+b-c=2p-2c}, a−b+c=2p−2b{\displaystyle a-b+c=2p-2b}, получаем:

h3=2(p−a)⋅2p⋅2(p−c)⋅2(p−b)4c2=4p(p−a)(p−b)(p−c)c2{\displaystyle {\begin{aligned}h^{2}&={\frac {2(p-a)\cdot 2p\cdot 2(p-c)\cdot 2(p-b)}{4c^{2}}}={\frac {4p(p-a)(p-b)(p-c)}{c^{2}}}\end{aligned}}}

Используя основное равенство для площади треугольника S=ch3{\displaystyle S={\frac {ch}{2}}} и подставляя в него полученное выражение для h, в итоге имеем:

S=c24⋅4p(p−a)(p−b)(p−c)c2=p(p−a)(p−b)(p−c){\displaystyle {\begin{aligned}S={\sqrt {{\frac {c^{2}}{4}}\cdot {\frac {4p(p-a)(p-b)(p-c)}{c^{2}}}}}={\sqrt {p(p-a)(p-b)(p-c)}}\end{aligned}}}

ч.т.д.

Эта формула содержится в «Метрике» Герона Александрийского (I век н. э.) и названа в его честь (хотя она была известна ещё Архимеду). Герон интересовался треугольниками с целочисленными сторонами, площади которых тоже являются целыми. Такие треугольники носят название героновых треугольников. Простейшим героновым треугольником является египетский треугольник.

• Выразив полупериметр через полусумму всех сторон данного треугольника, можно получить три эквивалентные формулы Герона:

S=14(a2+b2+c2)2−2(a4+b4+c4){\displaystyle S={\frac {1}{4}}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}}

S=142(a2b2+a2c2+b2c2)−(a4+b4+c4){\displaystyle S={\frac {1}{4}}{\sqrt {2(a^{2}b^{2}+a^{2}c^{2}+b^{2}c^{2})-(a^{4}+b^{4}+c^{4})}}}

S=14(a+b−c)(a−b+c)(−a+b+c)(a+b+c).{\displaystyle S={\frac {1}{4}}{\sqrt {(a+b-c)(a-b+c)(-a+b+c)(a+b+c)}}.}

S=144a2b2−(a2+b2−c2)2.{\displaystyle S={\frac {1}{4}}{\sqrt {4a^{2}b^{2}-(a^{2}+b^{2}-c^{2})^{2}}}.}

• Формулу Герона можно записать с помощью определителя в виде^[1]:

  −16S2=|0a2b21a20c21b2c2011110|=|abc0ba0cc0ab0cba|{\displaystyle -16S^{2}={\begin{vmatrix}0&a^{2}&b^{2}&1\\a^{2}&0&c^{2}&1\\b^{2}&c^{2}&0&1\\1&1&1&0\end{vmatrix}}={\begin{vmatrix}a&b&c&0\\b&a&0&c\\c&0&a&b\\0&c&b&a\end{vmatrix}}}

• Первый определитель последней формулы является частным случаем определителя Кэли — Менгера (англ.)русск. для вычисления гиперобъёма симплекса.

Аналоги формулы Герона[править | править код]

Имеются три формулы, по структуре аналогичные формуле Герона, но выражаемые в терминах других различных параметров треугольника.

• Первая формула выражает площадь через медианы, опущенные на стороны a, b и c, обозначенные соответственно через m_a, m_b и m_c, если их полусумма есть σ = (m_a + m_b + m_c)/2. Тогда мы имеем ^[2]

  S=43σ(σ−ma)(σ−mb)(σ−mc).{\displaystyle S={\frac {4}{3}}{\sqrt {\sigma (\sigma -m_{a})(\sigma -m_{b})(\sigma -m_{c})}}.}

• Обозначим высоты, проведенные к сторонам a, b и c треугольника соответственно через h_a, h_b и h_c, а полусумму их обратных величин обозначим через H=(ha−1+hb−1+hc−1)/2{\displaystyle H=(h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1})/2}. Тогда имеем ^[3]

S−1=4H(H−ha−1)(H−hb−1)(H−hc−1){\displaystyle S^{-1}=4{\sqrt {H(H-h_{a}^{-1})(H-h_{b}^{-1})(H-h_{c}^{-1})}}}

или в развернутом виде

S=1(1ha+1hb+1hc)(1hc+1hb−1ha)(1ha+1hc−1hb)(1ha+1hb−1hc){\displaystyle S={\frac {1}{\sqrt {({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}+{\frac {1}{h_{c}}})({\frac {1}{h_{c}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{a}}})({\frac {1}{h_{a}}}+{\frac {1}{h_{c}}}-{\frac {1}{h_{b}}})({\frac {1}{h_{a}}}+{\frac {1}{h_{b}}}-{\frac {1}{h_{c}}})}}}}

• Наконец, обозначим полусумму синусов углов треугольника через s = [(sin α) + (sin β) + (sin γ)]/2, тогда имеем ^[4]

S=D2s(s−sin⁡α)(s−sin⁡β)(s−sin⁡γ).{\displaystyle S=D^{2}{\sqrt {s(s-\sin \alpha )(s-\sin \beta )(s-\sin \gamma )}}.}

Здесь через D обозначен диаметр описанной окружности треугольника: D=asin⁡α=bsin⁡β=csin⁡γ.{\displaystyle D={\tfrac {a}{\sin \alpha }}={\tfrac {b}{\sin \beta }}={\tfrac {c}{\sin \gamma }}.}

где p=a+b+c+d2{\displaystyle p={\frac {a+b+c+d}{2}}} — полупериметр четырёхугольника. (Треугольник является предельным случаем вписанного четырёхугольника при устремлении длины одной из сторон к нулю. Например, при d=0)

• Та же Формула Брахмагупты через определитель^[5]:

  S=14−|abc−dba−dcc−dab−dcba|{\displaystyle S={\frac {1}{4}}{\sqrt {-{\begin{vmatrix}a&b&c&-d\\b&a&-d&c\\c&-d&a&b\\-d&c&b&a\end{vmatrix}}}}}

• Для тетраэдров верна формула Герона — Тарталья, которая обобщена также на случай других многогранников (см. изгибаемые многогранники): если у тетраэдра длины рёбер равны l1,l2,l3,l4,l5,l6{\displaystyle l_{1},l_{2},l_{3},l_{4},l_{5},l_{6}}, то для его объёма V{\displaystyle V} верно выражение

  144V2=l12l52(l22+l32+l42+l62−l12−l52){\displaystyle 144V^{2}=l_{1}^{2}l_{5}^{2}(l_{2}^{2}+l_{3}^{2}+l_{4}^{2}+l_{6}^{2}-l_{1}^{2}-l_{5}^{2})}+l22l62(l12+l32+l42+l52−l22−l62){\displaystyle +l_{2}^{2}l_{6}^{2}(l_{1}^{2}+l_{3}^{2}+l_{4}^{2}+l_{5}^{2}-l_{2}^{2}-l_{6}^{2})}+l32l42(l12+l22+l52+l62−l32−l42){\displaystyle +l_{3}^{2}l_{4}^{2}(l_{1}^{2}+l_{2}^{2}+l_{5}^{2}+l_{6}^{2}-l_{3}^{2}-l_{4}^{2})}−l12l22l42−l22l32l52−l12l32l62−l42l52l62{\displaystyle -l_{1}^{2}l_{2}^{2}l_{4}^{2}-l_{2}^{2}l_{3}^{2}l_{5}^{2}-l_{1}^{2}l_{3}^{2}l_{6}^{2}-l_{4}^{2}l_{5}^{2}l_{6}^{2}}.

• Предыдущая формула может быть выписана для тетраэдра в явном виде: Если U, V, W, u, v, w являются длинами ребер тетраэдра (первые три из них образуют треугольник; и , например, ребро u противоположно ребру U и т.д.), тогда справедливы формулы ^[6]

  V=(−a+b+c+d)(a−b+c+d)(a+b−c+d)(a+b+c−d)192uvw{\displaystyle {\text{V}}={\frac {\sqrt {\,(-a+b+c+d)\,(a-b+c+d)\,(a+b-c+d)\,(a+b+c-d)}}{192\,u\,v\,w}}}

где

a=xYZb=yZXc=zXYd=xyzX=(w−U+v)(U+v+w)x=(U−v+w)(v−w+U)Y=(u−V+w)(V+w+u)y=(V−w+u)(w−u+V)Z=(v−W+u)(W+u+v)z=(W−u+v)(u−v+W).{\displaystyle {\begin{aligned}a&={\sqrt {xYZ}}\\b&={\sqrt {yZX}}\\c&={\sqrt {zXY}}\\d&={\sqrt {xyz}}\\X&=(w-U+v)\,(U+v+w)\\x&=(U-v+w)\,(v-w+U)\\Y&=(u-V+w)\,(V+w+u)\\y&=(V-w+u)\,(w-u+V)\\Z&=(v-W+u)\,(W+u+v)\\z&=(W-u+v)\,(u-v+W).\end{aligned}}}

• Теорема Люилье. Площадь сферического треугольника выражается через его стороны θa=aR,θb=bR,θc=cR{\displaystyle \theta _{a}={\frac {a}{R}},\theta _{b}={\frac {b}{R}},\theta _{c}={\frac {c}{R}}} как:

  S=4R2arctg⁡tg⁡(θs2)tg⁡(θs−θa2)tg⁡(θs−θb2)tg⁡(θs−θc2){\displaystyle S=4R^{2}\,\operatorname {arctg} {\sqrt {\operatorname {tg} \left({\frac {\theta _{s}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{a}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{b}}{2}}\right)\operatorname {tg} \left({\frac {\theta _{s}-\theta _{c}}{2}}\right)}}}, где θs=θa+θb+θc2{\displaystyle \theta _{s}={\frac {\theta _{a}+\theta _{b}+\theta _{c}}{2}}} — полупериметр.

1. ↑ Weisstein, Eric W. Heron’s Formula. From MathWorld—A Wolfram Web Resource.
2. ↑ Benyi, Arpad, «A Heron-type formula for the triangle,» Mathematical Gazette» 87, July 2003, 324–326.
3. ↑ Mitchell, Douglas W., «A Heron-type formula for the reciprocal area of a triangle,» Mathematical Gazette 89, November 2005, 494.
4. ↑ Mitchell, Douglas W., «A Heron-type area formula in terms of sines,» Mathematical Gazette 93, March 2009, 108–109.
5. ↑ Стариков В.Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 37-39
6. ↑ W. Kahan, «What has the Volume of a Tetrahedron to do with Computer Programming Languages?», [1], pp. 16-17.

• §258 в А. П. Киселёв, «Геометрия по Киселёву», arΧiv:1806.06942v3 [math.HO] 

• Николаев Н. О площади треугольника (рус.) // В.О.Ф.Э.М.. — 1890. — № 108. — С. 227—228.
• Raifaizen, Claude H. A Simpler Proof of Heron’s Formula (англ.) // Mathematics Magazine : magazine. — 1971. — Vol. 44. — P. 27—28. — доказательство формулы Герона на основе теоремы Пифагора