Сфера в 2: что это такое, техника и система, отличия от сегмента B2C – B2b — Википедия
Сфера — Википедия
 Сфера (каркасная проекция)
Сфера (каркасная проекция)
 Сфера — поверхность шара
Сфера — поверхность шара
Сфе́ра (др.-греч. σφαῖρα «мяч, шар[1]») — геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).
Расстояние от точки сферы до её центра называется радиусом сферы.
Сфера радиуса 1 называется единичной сферой.
Сфера является поверхностью вращения, образованной при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учётом непостоянства значения размеров дуг составляет 41252,96 кв. градусов.
Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны.
Сфера является поверхностью шара. Сфера имеет наименьшую площадь из всех поверхностей, ограничивающих данный объём, также из всех поверхностей с данной площадью сфера ограничивает наибольший объём. Поэтому тела сферической формы встречаются в природе, например, маленькие капли воды при свободном падении приобретают сферическую форму именно из-за минимизации площади поверхности силой поверхностного натяжения.
Объём цилиндра, объём вписанного в него шара, касающегося обоих его оснований, и объём конуса, с вершиной в центре одного основания цилиндра и с основанием, совпадающим с другим основанием цилиндра, находятся в соотношении 3 : 2 : 1[2].
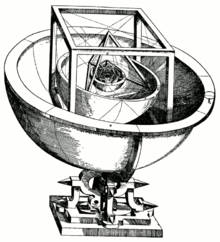 «Кубок Кеплера»: модель Солнечной системы из пяти правильных многогранников и их вписанных и описанных сфер.
«Кубок Кеплера»: модель Солнечной системы из пяти правильных многогранников и их вписанных и описанных сфер.
Совершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира. Древнегреческий учёный Пифагор вместе с шарообразной Землёй в центре Вселенной ввёл окружающую Землю удалённую хрустальную сферу, к которой прикреплены звёзды, и семь более близких вращающихся хрустальных сфер, к которым прикреплены Солнце, Луна и пять известных к тому времени планет (исключая Землю). Эта модель впоследствии усложнялась: Евдокс Книдский рассматривал уже 27 подобных сфер, а Аристотель — 55 хрустальных сфер
[3]. Представления о вращающихся небесных сферах господствовали по крайней мере до средних веков и даже вошли в гелиоцентрическую систему мира Николая Коперника, который назвал свой основной труд «О вращении небесных сфер» (лат. De revolutionibus orbium coelestium).
Небесные сферы со времён Древней Греции были частью более общей концепции гармонии сфер о музыкально-астрономическом устройстве мира, куда также входило понятие «музыка сфер». Эта концепция также существовала как минимум до средневековья. У одного из известнейших астрономов, Иоганна Кеплера, сфера занимала центральное место во всей его системе религиозно-мистических представлений, он писал: «Образ триединого бога есть сферическая поверхность, а именно: бог-отец в центре, бог-сын — на поверхности и святой дух — в симметричном отношении между центром и описанной вокруг него сферической поверхностью»
[7]. Как удобная математическая модель, осталась одна небесная сфера, с помощью которой астрономы по сей день представляют видимые положения звезд и планет.
Уравнение сферы в прямоугольной системе координат:
- (x−x0)2+(y−y0)2+(z−z0)2=R2,{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},}
где (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})} — координаты центра сферы, R{\displaystyle R} — её радиус.
Параметрическое уравнение сферы с центром в точке (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})}:
- {x=x0+R⋅sinθ⋅cosϕ,y=y0+R⋅sinθ⋅sinϕ,z=z0+R⋅cosθ,{\displaystyle {\begin{cases}x=x_{0}+R\cdot \sin \theta \cdot \cos \phi ,\\y=y_{0}+R\cdot \sin \theta \cdot \sin \phi ,\\z=z_{0}+R\cdot \cos \theta ,\\\end{cases}}}
где θ∈[0,π]{\displaystyle \theta \in [0,\pi ]} и ϕ∈[0,2π).{\displaystyle \phi \in [0,2\pi ).}
Гауссова кривизна сферы постоянна и равна 1/R².
Основные геометрические формулы[править | править код]
- Площадь поверхности сферы
- S=4πr2=πd2.{\displaystyle S=4\pi r^{2}=\pi d^{2}.}
- Объём шара, ограниченного сферой
- V=43πr3.{\displaystyle V={\frac {4}{3}}\pi r^{3}.}
- Площадь сегмента сферы высоты H{\displaystyle H}
- S=2πrH{\displaystyle S=2\pi rH}.
Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие окружности являются геодезическими линиями на сфере; любые две из них пересекаются в двух точках. Иными словами, большие круги сферы являются аналогами прямых на плоскости, расстояние между точками на сфере — длина дуги проходящего через них большого круга. Углу же между прямыми на плоскости соответствует двугранный угол между плоскостями больших кругов. Многие теоремы геометрии на плоскости справедливы и в сферической геометрии, существуют аналоги теоремы синусов, теоремы косинусов для сферических треугольников. В то же время, существует немало отличий, например, в сферическом треугольнике сумма углов всегда больше 180 градусов, к трём признакам равенства треугольников добавляется их равенство по трём углам, у сферического треугольника может быть два и даже три прямых угла — например, у сферического треугольника, образованного экватором и меридианами 0° и 90°.
Расстояние между двумя точками на сфере[править | править код]
Если даны сферические координаты двух точек, то расстояние между ними можно найти так:
- L=R⋅arccos(cosθ1⋅cosθ2+sinθ1⋅sinθ2⋅cos(ϕ1−ϕ2)).{\displaystyle L=R\cdot \arccos(\cos \theta _{1}\cdot \cos \theta _{2}+\sin \theta _{1}\cdot \sin \theta _{2}\cdot \cos(\phi _{1}-\phi _{2})).}
Однако, если угол θ{\displaystyle \theta } задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:
- L=R⋅arccos(sinθ1⋅sinθ2+cosθ1⋅cosθ2⋅cos(ϕ1−ϕ2)).{\displaystyle L=R\cdot \arccos(\sin \theta _{1}\cdot \sin \theta _{2}+\cos \theta _{1}\cdot \cos \theta _{2}\cdot \cos(\phi _{1}-\phi _{2})).}
В этом случае θ1{\displaystyle \theta _{1}} и θ2{\displaystyle \theta _{2}} называются широтами, а ϕ1{\displaystyle \phi _{1}} и ϕ2{\displaystyle \phi _{2}} долготами.
В общем случае уравнение (n−1)-мерной сферы (в n-мерном евклидовом пространстве) имеет вид:
- ∑i=1n(xi−ai)2=r2,{\displaystyle \sum _{i=1}^{n}(x_{i}-a_{i})^{2}=r^{2},}
где (a1,…,an){\displaystyle (a_{1},…,a_{n})} — центр сферы, а r{\displaystyle r} — радиус.
Пересечением двух n-мерных сфер является (n−1)-мерная сфера, лежащая на радикальной гиперплоскости этих сфер.
В n-мерном пространстве могут попарно касаться друг друга (в разных точках) не более n+1
сфер.
n-мерная инверсия переводит (n−1)-мерную сферу в (n−1)-мерную сферу или гиперплоскость.
С трёхмерной сферой связана одна из задач тысячелетия — гипотеза Пуанкаре, в которой утверждается, что всякое односвязное компактное трёхмерное многообразие без края гомеоморфно такой сфере. Эта гипотеза была доказана Г. Я. Перельманом в начале 2000-х годов на основе результатов Ричарда Гамильтона.
Класс гомеоформности компактной триангулируемой поверхности определяется ориентируемостью, числом компонент границы и эйлеровой характеристикой. | |
| Без границы | |
| С границей | |
| Связанные понятия | |
Сфера 2: Арена — Википедия
Материал из Википедии — свободной энциклопедии
«Сфера 2: Арена» — это бесплатная онлайновая фэнтезийная MMORPG, ориентированная на сражениях игроков между собой на аренах. C 30 ноября 2012 года игра официально закрыта, сервера отключены[1].
Главным отличием «Сфера II: Арена» от других MMORPG является игровая модель, ориентированная на сражения между игроками и кланами игроков. В «Сфере 2: Арена» не существует мобов пригодных для сражения, как в большинстве популярных онлайн-играх. Не существует и мира, который можно исследовать. Единственные персонажи в игре, которые управляются искусственным интеллектом — это торговцы[2]. Однако, торговать можно не только с NPC — возможно обмена между игроками появляется у персонажей на 2 уровне, а с 3 уровня игроки могут объединяться в кланы.
В игре присутствуют две расы, у каждой из которых есть четыре игровых класса[3].
- Врилы — вампиры. С их расой связаны многие предрасудки. Они не боятся света, серебра, чеснока и не превращаются в летучую мышь.
- Люди — люди первоначальное население мира «Сфера».
В игре имеется три арены[4]:
- Теснина Мертвецов (синий портал). Тип арены — захват флага. Играть и устанавливать ограничения можно на разные уровни, можно задавать пароль. Особенность Арены — замок врилов, на котором можно запрыгнуть на арматурную колону, что даёт преимущество при похищении или укрывательстве флага.
- Чужая Святыня (красный портал). Тип арены — накопление ресурсов. Главная цель — захват и удержание кристаллов до окончания времени сражения или же набирание определённого количества ресурсов. Захват кристалла требует времени и возможен только в неподвижном состоянии. Атакуя игрока можно сбить захват. Отличительная особенность от синей арены в том, что здесь есть стена, защищающая респаун от противника.
- Без названия. Тип арены — Team Deathmatch. На арене могут участвовать только персонажи выше 5 уровня. Особенность этой арены в возможности играть 1 на 1, на ней нет опыта, рейтинга и денег, поэтому она считается идеальной для дуэлей.
Типы сражений[править | править код]
Всего существует четыре вида сражений:
- Свободный — люди и врилы сражаются в одной команде;
- Клановый — сражения между кланами;
- Расовый — люди и врилы сражаются друг против друга.
- Бой за торговца — бой за покровительство над торговцем. Бои проходят в синей или красной аренах, максимум по 10 человек от клана.
О компании
Купить продукцию нашей компании – означает обеспечить собственное производство высокотехнологичными изделиями российского и зарубежного производства. Предлагаемая нами продукция надежная, долговечная, качественная, соответствует международным нормам и стандартам.
Ассортимент
Предприятие ООО «Сфера2К» на протяжении многих лет уверенно работает на промышленном рынке Смоленска, всего западного региона России. Компания является лидером по обеспечению ведущих производственных сфер Смоленщины и России в целом.
Перерабатывающие компании пользуются нашим эффективным сервисом для снабжения своих производств основными комплектующими изделиями:
- ремнями всех типоразмеров;
- остродефицитными подшипниками;
- оргстеклом;
- манжетами, хомутами, метизами;
- паронитом, капролоном, другими материалами, запчастями.
Преимущества
Выгоды от сотрудничества с нашей компанией существенны и неоспоримы:
- реальную экономию времени и денег вам принесет наличие у нас склада и офиса в одном месте;
- складское хозяйство предприятия содержит колоссальный ассортимент продукции, предназначенной для реализации;
- расчеты осуществляются в удобной для клиентов форме: безналичными, наличными в кассе;
- короткие сроки, полнейшая комплектация товаров;
- оригинальность продукции подтверждается выдачей паспортов качества, сертификатов соответствия;
- постоянным заказчикам предоставляются: отсрочки платежей, скидки, бесплатные консультации ведущих специалистов.
Покупая комплектующие и запчасти у нас, вы будете иметь полную уверенность в уникальности продукции, поскольку мы приобретаем товар у непосредственных производителей. Это позволяет напрямую контролировать качество и удерживать стоимость в низком ценовом диапазоне.
Трёхмерная сфера — Википедия
Материал из Википедии — свободной энциклопедии
Стереографическая проекция параллелей гиперсферы (красная), меридианов (синий) и гипермеридианов (зелёный). В связи с конформными свойствами стереографической проекции, кривые пересекаются друг с другом ортогонально (в жёлтых точках), как в 4D. Все кривые являются окружностями: кривые, которые пересекаются имеют бесконечный радиус (то есть являются прямыми).
Трёхмерная сфера, или трёхмерная гиперсфера, иногда 3-сфера, — сфера в четырёхмерном пространстве. Состоит из множества точек, равноудалённых от фиксированной центральной точки в четырёхмерном евклидовом пространстве. Так же, как двумерная сфера, которая образует границу шара в трёх измерениях, 3-сфера имеет три измерения и является границей четырёхмерного шара.
В декартовых координатах (x0,x1,x2,x3){\displaystyle (x_{0},x_{1},x_{2},x_{3})} трёхмерная сфера радиуса r{\displaystyle r} может быть задана уравнением
- (x0−C0)2+(x1−C1)2+(x2−C2)2+(x3−C3)2=r2.{\displaystyle (x_{0}-C_{0})^{2}+(x_{1}-C_{1})^{2}+(x_{2}-C_{2})^{2}+(x_{3}-C_{3})^{2}=r^{2}.}
Рассматривая комплексное пространство C2{\displaystyle \mathbb {C} ^{2}} как вещественное R4{\displaystyle \mathbb {R} ^{4}}, уравнение сферы может быть рассмотрено как
- S3={(z1,z2)∈C2:|z1|2+|z2|2=1}.{\displaystyle S^{3}=\left\{(z_{1},z_{2})\in \mathbb {C} ^{2}:|z_{1}|^{2}+|z_{2}|^{2}=1\right\}.}
Аналогично, в пространстве кватернионов h2{\displaystyle \mathbb {H} ^{1}}:
- S3={q∈H:‖q‖=1}.{\displaystyle S^{3}=\left\{q\in \mathbb {H} :\|q\|=1\right\}.}
Являясь трёхмерным многообразием, трёхмерная сфера может быть задана параметрически с использованием трёх координат. Примером являются гиперсферические координаты:
- x0=rcosψ,{\displaystyle x_{0}=r\cos \psi ,}
- x1=rsinψcosθ,{\displaystyle x_{1}=r\sin \psi \cos \theta ,}
- x2=rsinψsinθcosϕ,{\displaystyle x_{2}=r\sin \psi \sin \theta \cos \phi ,}
- x3=rsinψsinθsinϕ.{\displaystyle x_{3}=r\sin \psi \sin \theta \sin \phi .}
Трёхмерная сфера S3{\displaystyle S^{3}} является границей четырёхмерного шара.
Трёхмерная сфера является компактным связным трёхмерным многообразием. Трёхмерная сфера односвязна, то есть любая замкнутая кривая на неё может быть непрерывно стянута в точку.
Трёхмерная сфера гомеоморфна одноточечной компактификации трёхмерного вещественного пространства R3{\displaystyle \mathbb {R} ^{3}}.
Являясь множеством единичных кватернионов, трёхмерная сфера наследует групповую структуру.
Таким образом, сфера S3{\displaystyle S^{3}} является группой Ли. Среди n{\displaystyle n}-мерных сфер таким свойством обладают только S1{\displaystyle S^{1}} и S3{\displaystyle S^{3}}.
Используя матричное представление кватернионов, можно определить представление группы S3{\displaystyle S^{3}} с помощью матриц Паули:
- x1+x2i+x3j+x4k↦(x1+ix2x3+ix4−x3+ix4x1−ix2).{\displaystyle x_{1}+x_{2}i+x_{3}j+x_{4}k\mapsto {\begin{pmatrix}\;\;\,x_{1}+ix_{2}&x_{3}+ix_{4}\\-x_{3}+ix_{4}&x_{1}-ix_{2}\end{pmatrix}}.}
Поэтому группа S3{\displaystyle S^{3}} изоморфна матричной группе Ли SU(2){\displaystyle \mathrm {SU} (2)}.
Действие группы U(1) и расслоение Хопфа[править | править код]
Если определить действие группы U(1){\displaystyle U(1)}:
- (z1,z2)⋅λ=(z1λ,z2λ)∀λ∈U(1),{\displaystyle (z_{1},z_{2})\cdot \lambda =(z_{1}\lambda ,z_{2}\lambda )\quad \forall \lambda \in \mathbb {U} (1),}
то пространство орбит гомеоморфно двумерной сфере S2{\displaystyle S^{2}}. При этом на сфере S3{\displaystyle S^{3}} возникает структура расслоения с базой S2{\displaystyle S^{2}} и слоями, гомеоморфными U(1){\displaystyle U(1)}, то есть окружности S1{\displaystyle S^{1}}. Это расслоение называется расслоением Хопфа.[1]
Расслоение Хопфа является примером нетривиального главного расслоения. В координатах оно задаётся формулой
- p:(z1,z2)↦(z1:z2).{\displaystyle p:(z_{1},z_{2})\mapsto (z_{1}:z_{2}).}
Точка (z1, z2) сферы S3{\displaystyle S^{3}} отображается в точку [z1: z2] комплексной проективной прямой CP1, которая диффеоморфна двумерной сфере S2{\displaystyle S^{2}}.
Односвязность сферы означает, что первая гомотопическая группа π1(S3)={0}{\displaystyle \pi _{1}(S^{3})=\{0\}}. Также нулевой является группа π2(S3)={0}{\displaystyle \pi _{2}(S^{3})=\{0\}}.
- ↑ Постников М. М. Лекции по алгебраической топологии, с. 20. — Москва, Наука, 1984.
- Фоменко А. Т., Фукс Д. Б. Курс гомотопической топологии. — М., 1989.
- Weisstein, Eric W. Hypersphere (англ.) на сайте Wolfram MathWorld. (англ.) Примечание: В данной статье используются альтернативные схемы именования для сфер, в которых сфера в N-мерном пространстве называется N-сферой.
