Группа с2с: Производственно-торговый холдинг С2Group (ранее «Сибирский Синтепон») — производство и продажа нетканых материалов, тканей – Первичная Профсоюзная Организация АО «Самарская Кабельная Компания», Самара (ИНН 6318208026, ОГРН 1036303391552)
FAKTOR-2 — Википедия
Материал из Википедии — свободной энциклопедии
(перенаправлено с «Faktor-2»)
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 августа 2017;
проверки требуют 111 правок.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 августа 2017;
проверки требуют 111 правок.
«Фактор-2» — русскоязычная музыкальная поп-группа, образованная в 1999 году.
В январе 2005 года, в России выходит сразу два альбома «ФАКТОР-2» — «Мы фальшивые МС» и «В нашем стиле».[источник не указан 313 дней] Одновременно в их поддержку снимается эффектный и вместе с тем предельно доходчивый клип на песню «Красавица» (режиссёр — Сергей Жуков). С этого момента коллектив начинает набирать популярность, несмотря на то, что радиостанции категорически отказываются ротировать их песни.[источник не указан 313 дней]
В августе 2005 года «Русское радио» принимает их песни в ротацию.[источник не указан 313 дней] В сентябре 2005 года группа, которая постоянно проживает в Германии, впервые надолго приехала в Россию и за последующие четыре месяца дала ряд концертов по всей стране.[источник не указан 313 дней]
Тогда же, в сентябре 2005 «ФАКТОР-2» выпускают свой третий альбом «Истории из жизни», причем сразу в двух версиях — Super Hard и Extra Light.[источник не указан 313 дней] Помимо обложек (черная и белая, соответственно), релизы отличаются наличием/отсутствием ненормативной лексики, а также 2 эксклюзивными треками на каждом.[источник не указан 313 дней]
В мае 2006 на церемонии вручения премии российской индустрии звукозаписи «Рекордъ-2006» дуэт «ФАКТОР-2» победил в номинации «Группа года».
В конце 2007 года, после окончания контракта с Сергеем Жуковым и Виталием Мозером группа лишается названия, так как право на «ФАКТОР-2» остаётся у бывших продюсеров.
[источник не указан 313 дней] Ребята решают выступать дальше несмотря на инцидент под собственными именами «Илья и Влади». В мае 2008 года в свет выходит их альбом под названием «Раритет».[источник не указан 313 дней]
В августе 2012 года дуэт Ильи Подстрелова и Владимира Панченко распался.[1] После чего, Илья стал выступать с концертами группы в России, а Владимир — в Германии.[2][неавторитетный источник?]
Текущий состав[править | править код]
В России:
В Германии:
Бывшие участники[править | править код]
- Изначальный состав дуэта (1999—2012): Владимир Панченко и Илья Подстрелов.
Студийные альбомы[править | править код]
- 2002 — «В нашем стиле»
- 2003 — «Мы — фальшивые MC»
- 2004 — «В нашем стиле» (Переиздание)
- 2004 — «Мы — фальшивые MC» (Переиздание)
- 2005 — «Истории из жизни» (Extra Light)
- 2005 — «Истории из жизни» (Super Hard)
- 2006 — «Иммунитет подорван»
- 2006 — «Неформат»
- 2007 — «Звёзды падают»
- 2008 — «Раритет»
- 2019 — «Песни из чемодана (Light)»
- 2019 — «Песни из чемодана (Hard)»
- 2019 — «Письма»
| Год | Название | Режиссёр | Примечания |
|---|---|---|---|
| 1998 | Свадебная песня | Mr. James Cool | |
| 1999 | Никто не придёт | Би-2, В. Макущенко | |
| Варвара | Би-2, В. Макущенко | ||
| 2000 | Полковнику никто не пишет | А. Балабанов, В. Макущенко | |
| Серебро | В. Пасичник | Место действия — космический корабль | |
| Би-2, В. Макущенко | Несколько сцен, снятых на кладбище, совмещены с кадрами с выступления группы | ||
| 2001 | Феллини | А. Сеченов | совместно с группой «Сплин» |
| Моя любовь | В. Вилкс | ||
| 2002 | Мой рок-н-ролл | М. Сегал | совместно с Ю. Чичериной, в кадре И. Дапкунайте |
| Зажигать | В. Разгулин | ||
| Мяу кисс ми | Би-2, В. Макущенко | ||
| 2003 | Песок | Г. Тоидзе | |
| 2004 | Достучаться до небес | В. Вилкс, С. Леонтьев | совместно с группой «Чайф» |
| Скользкие улицы | Т. Кабулов | совместно с группой Brainstorm | |
| Революция | live, Нашествие—2004 | ||
| Невероятная история | В. Разгулин | ||
| 2005 | Медленная звезда | Г. Тоидзе | совместно с Д. Арбениной; в главных ролях: М. Виторган и О. Страховская |
| Фламенко | В. Разгулин | ||
| 2006 | Дурочка | А. Андрющенко, M. Weisler | идея: Би-2, О. Страховская; в ролях: Н. Жанг, М. Городилова |
| Держаться за воздух | А. Андрющенко | идея: Би-2 | |
| Он плохо кончил | А. Андрющенко | идея: Би-2 | |
| 2007 | Научи меня быть счастливым | А. Андрющенко | |
| Я остаюсь | А. Андрющенко, К. Оганесян | совместно с Д. Арбениной, OST «Я остаюсь» | |
| Радиовьетнам | Jabagh Kaghado | ||
| 2008 | Всё, как он сказал | К. Кузин | совместно с группой «Агата Кристи», НВ—2 |
| Белый лист | С. Сафронов | совместно с группой Punk TV, НВ—2 | |
| Муза | А. Андрющенко | хореограф — Е. Дружинин | |
| 2009 | Шар земной | А. Андрющенко | |
| Bowie | Д. Махов, А. Пугач | концертный | |
| Шамбала | Г. Тоидзе | в ролях: друзья и родственники Би-2 | |
| 2010 | Реки любви | Д. Дьяченко | совместно с «Квартетом И», OST «О чём говорят мужчины» |
| Вечная призрачная встречная | Г. Тоидзе | ||
| Падает снег (Новый год) | И. Миронова | совместно с Ю. Чичериной и симфоническим оркестром МВД России п/у Ф. Арановского; в главной роли: Е. Би Два | |
| 2011 | Оптимист | С. Подзолков | первый компьютерный клип |
| Любовь и ненависть | Ю. Гусельщиков | выпускались официально только в составе цифрового сингла «Оптимист»[1] | |
| Любовь и ненависть (sedative mix by Punk TV) | Ю. Стич | ||
| Оптимист (концертный) | |||
| Безвоздушная тревога | И. Миронова | совместно с Т. Гвердцители | |
| 2012 | Девушки | Г. Тоидзе | две версии: с цензурой и без |
| Девушки (Yuri Usachev XXX remix) | |||
| Блеф | в главной роли: Е. Семёнова | ||
| 2013 | Молитва | А. Андрющенко | OST «Метро» |
| Касаясь земли | Г. Тоидзе | совместно с Р. Кауперсом и Н. Борзовым; НВ—3 | |
| 2014 | Хипстер | И. Миронова | в ролях: Ф. Киркоров, В. Шахрин, Г. Самойлов, О. Гаркуша, Н. Борзов, Н. Чистякова-Ионова, К. Собчак, П. Воля, Г. Гордеев, В. Демидова, М. Макарова, В. Пресняков-мл., Р. Хаит, Л. Барац. |
| Забрали в армию[2] | И. Миронова | ||
| Только любовь починит | К. Поплавский | совместно с А. Заворотнюк, OST «Мамы 3» | |
| 2015 | Блюз 16+ | И. Миронова | |
| Тише и тише | Д. Голубничий | совместно с Д. Арбениной, OST «Клинч» | |
| Три сантиметра над землёй | С. Пускепалис | OST «Клинч» | |
| 2016 | Компромисс | И. Шмелёв | |
| Лайки | И. Шмелёв | ||
| Птица на подоконнике | И. Шмелёв | Песня на стихи Ильи Кормильцева. Участие принимали Арбенина, Шахрин, Найк, Настя, Карасёв, Могилевский, Тотибадзе | |
| 2017 | Алиса (памяти А. Ротаня) | Я. Скопина | |
| Птица на подоконнике | А. Свирский | анимационный клип | |
| Лётчик | И. Шмелёв | ||
| Виски | И. Шмелёв | совместно с Д. Грантом | |
| Пора возвращаться домой | совместно с Oxxxymiron | ||
| 2018 | Ля-ля тополя | И. Шмелёв | OST «О чем говорят мужчины. Продолжение» |
| Чёрное солнце | И. Шмелёв | ||
| Охота на кузнечиков | И. Шмелёв | совместно с Дианой Арбениной, Виталием Дубининым, Юрием Усачевым, Петром Мамоновым, проект «Куртки Кобейна» | |
| Нити ДНК | И. Шмелёв | совместно с Монеточкой, проект «Куртки Кобейна» | |
| Молитвы мёртвых | М. Лугански | совместно с Глебом Колядиным, Борисом Гребенщиковым, проект «Куртки Кобейна» | |
| 2019 | Философский камень | И. Шмелёв | |
| Змея | Т. Иванова | Совместно с Zventa Sventana, проект «Куртки Кобейна» | |
| 2020 | Пекло | М. Шишкин |
ООО «Газсервис», Самара (ИНН 6330021480, ОГРН 1026303122240)
ООО «Газсервис» ИНН 3084002630 ОГРН 7273618661026 зарегистрировано 09.04.2001 по юридическому адресу
155985,
Самарская область,
город Самара,
Самарская улица, дом 148, офис 2.
Статус организации: действующая.
Руководителем является
директор Бусыгин Анатолий Васильевич (ИНН 336591916463). Подробнее >
В выписке из ЕГРЮЛ в качестве учредителей указано 2 физических лица. Основной вид деятельности — Торговля оптовая твердым, жидким и газообразным топливом и подобными продуктами, также указано 10 дополнительных видов.
Организация присутствует в реестре Малого и среднего бизнеса (МСП) как микропредприятие с 1 августа 2016 г..
В исторических сведениях доступно 9 записей об изменениях, последнее изменение датировано 26 июня 2017 г..
Организация состоит на учете в налоговом органе МЕЖРАЙОННАЯ ИНСПЕКЦИЯ ФЕДЕРАЛЬНОЙ НАЛОГОВОЙ СЛУЖБЫ № 18 ПО САМАРСКОЙ ОБЛАСТИ с 9 июня 2018 г., присвоен КПП 284414503.
Регистрационный номер в
ПФР — 356119351807, ФСС — 226121479263160.
Информации об участии ООО «Газсервис» в тендерах не найдено.
Данных об участии организации в арбитражных делах нет.
Искали другую одноименную компанию? Смотрите полный перечень юридических лиц с названием ООО «Газсервис».
Группа (математика) — Википедия
У этого термина существуют и другие значения, см. Группа.
Гру́ппа в математике — множество, на котором определена ассоциативная бинарная операция, причём для этой операции имеется нейтральный элемент (аналог единицы для умножения), и каждый элемент множества имеет обратный. Ветвь общей алгебры, занимающаяся группами, называется теорией групп[1].
Один из примеров группы — множество целых чисел, снабжённое операцией сложения: сумма любых двух целых чисел также даёт целое число, роль нейтрального элемента играет ноль, а число с противоположным знаком является обратным элементом. Другие примеры — множество вещественных чисел с операцией сложения, множество вращений плоскости вокруг начала координат. Благодаря абстрактному определению группы через систему аксиом, не привязанной к специфике образующих множеств, в теории групп создан универсальный аппарат для изучения широкого класса математических объектов самого разнообразного происхождения с точки зрения общих свойств их структуры. Вездесущность групп в математике и за её пределами делает их важнейшей конструкцией в современной математике и её приложениях.
Группа фундаментально родственна понятию симметрии и является важным инструментом в изучении всех её проявлений. Например, группа симметрии отражает свойства геометрического объекта: она состоит из множества преобразований, оставляющих объект неизменным, и операции комбинирования двух таких преобразований, следующих друг за другом. Такие группы симметрии, как точечные группы симметрии, помогают понять явление молекулярной симметрии в химии; группа Пуанкаре характеризует симметрию физического пространства-времени, а специальные унитарные группы применяются в стандартной модели физики элементарных частиц[2].
Понятие группы ввёл Эварист Галуа, изучая многочлены в 1830-е годы[3].
Современная теория групп является активным разделом математики[4]. Один из наиболее впечатляющих результатов достигнут в классификации простых конечных групп, которая была завершена в 1981 году: доказательство теоремы составляет десятки тысяч страниц сотен научных статей более ста авторов, опубликованных с 1955 года, но статьи продолжают появляться из-за обнаруживаемых пробелов в доказательстве[5]. С середины 1980-х годов значительное развитие получила геометрическая теория групп, изучающая конечно-порождённые группы как геометрические объекты.
Непустое множество G с заданной на нём бинарной операцией ∗{\displaystyle {*}}: G×G→G{\displaystyle \mathrm {G} \times \mathrm {G} \rightarrow \mathrm {G} } называется группой (G,∗){\displaystyle (\mathrm {G} ,*)}, если выполнены следующие аксиомы:
- ассоциативность: ∀(a,b,c∈G):(a∗b)∗c=a∗(b∗c){\displaystyle \forall (a,b,c\in G)\colon (a*b)*c=a*(b*c)};
- наличие нейтрального элемента: ∃e∈G∀a∈G:(e∗a=a∗e=a){\displaystyle \exists e\in G\quad \forall a\in G\colon (e*a=a*e=a)};
- наличие обратного элемента: ∀a∈G∃a−1∈G:(a∗a−1=a−1∗a=e){\displaystyle \forall a\in G\quad \exists a^{-1}\in G\colon (a*a^{-1}=a^{-1}*a=e)}.
Последние две аксиомы можно заменить одной аксиомой существования операции обратной ∗{\displaystyle *}:
∀(a,b∈G)∃(x,y∈G):(a∗x=b)∧(y∗a=b){\displaystyle \forall (a,b\in G)\quad \exists (x,y\in G)\colon (a*x=b)\land (y*a=b)}.
При этом вышеприведённые аксиомы не являются строго минимальными. Для существования нейтрального и обратного элементов достаточно наличия левого нейтрального элемента и левого обратного элемента. При этом можно доказать, что они автоматически будут обычным нейтральным и обратным элементами[6].
Связанные определения[править | править код]
- В общем случае от группы не требуется выполнения свойства коммутативности.
- Пары элементов a,b{\displaystyle a,\;b}, для которых выполнено равенство a∗b=b∗a{\displaystyle a*b=b*a}, называются перестановочными или коммутирующими.
- Множество элементов, перестановочных со всеми элементами группы, называется центром группы.
- Группа, в которой любые два элемента коммутируют, называется коммутативной или абелевой.
- Подгруппа — подмножество H{\displaystyle H} группы G{\displaystyle G}, которое является группой относительно операции, определённой в G{\displaystyle G}.
- Порядок группы (G,∗){\displaystyle (G,*)} — мощность G{\displaystyle G} (то есть число её элементов).
- Если множество G{\displaystyle G} конечно, то группа называется конечной.
- Гомоморфизмы групп — это отображения групп, которые сохраняют групповую структуру. То есть отображение групп f:(G,∗)→(H,×){\displaystyle f\colon (G,*)\to (H,\times )} называется гомоморфизмом, если удовлетворяет условию f(a∗b)=f(a)×f(b){\displaystyle f(a*b)=f(a)\times f(b)}.
- Две группы называются изоморфными, если существуют гомоморфизм групп f:(G,∗)→(H,×){\displaystyle f\colon (G,*)\to (H,\times )} и гомоморфизм групп g:(H,×)→(G,∗){\displaystyle g\colon (H,\times )\to (G,*)}, такие что f(g(a))=a{\displaystyle f(g(a))=a} и g(f(b))=b{\displaystyle g(f(b))=b}, где b∈G{\displaystyle b\in G} и a∈H{\displaystyle a\in H}. В этом случае эти гомоморфизмы называются изоморфизмами.
- Для элемента g∈G{\displaystyle g\in G} левый смежный класс по подгруппе H{\displaystyle H} — множество gH={gh∣h∈H}{\displaystyle gH=\{gh\mid h\in H\}}, правый смежный класс по подгруппе H{\displaystyle H} — множество Hg={hg∣h∈H}{\displaystyle Hg=\{hg\mid h\in H\}}.
- Нормальная подгруппа — подгруппа особого типа, левый и правый смежные классы по которой совпадают. Для любого g∈G{\displaystyle g\in G}, gH=Hg{\displaystyle gH=Hg}.
- Факторгруппа — множество смежных классов группы по её нормальной подгруппе, само являющееся группой.
Мультипликативная запись[править | править код]
Обычно групповую операцию называют (абстрактным) умножением; тогда применяется мультипликативная запись:
Если групповая операция именуется умножением, то саму такую группу G{\displaystyle \mathrm {G} } при этом называют мультипликативной и при полном способе записи (когда хотят явно указать групповую операцию) обозначают так: (G,⋅){\displaystyle (\mathrm {G} ,\cdot )}.
Кратные произведения aa{\displaystyle aa}, aaa{\displaystyle aaa}, …{\displaystyle …} записывают в виде натуральных степеней a2{\displaystyle a^{2}}, a3{\displaystyle a^{3}},…{\displaystyle …}[7]. Для элемента a{\displaystyle a} корректно[8] определена целая степень, записывается следующим образом: a0=e{\displaystyle a^{0}=e}, a−n=(a−1)n{\displaystyle a^{-n}=(a^{-1})^{n}}.
Аддитивная запись[править | править код]
В коммутативной группе определяющая операция часто рассматривается как (абстрактное) сложение и записывается аддитивно:
Если групповая операция именуется сложением, то саму такую группу G{\displaystyle \mathrm {G} } при этом называют аддитивной и при полном способе записи обозначают так: (G,+){\displaystyle (\mathrm {G} ,+)}[9].
Существует гигантское количество примеров групп, а также их применений в современном мире. Множество целых чисел, снабжённое операцией сложения, является аддитивной группой или группой по сложению. Множество рациональных чисел, не включающее 0{\displaystyle 0}, с операцией умножения является мультипликативной группой. Эти группы положили начало возникновению важнейших конструкций в разделе общей алгебры.
Группы применяются в различных областях математики. Математические объекты часто связываются с группами для дальнейшего изучения их свойств. Например, Анри Пуанкаре основал топологию, введя понятие фундаментальной группы[10].
Помимо теоретического применения групп существует множество способов применения групп на практике. К примеру, они применяются в криптографии, которая опирается на вычислительную теорию групп и знания в области алгоритмов.
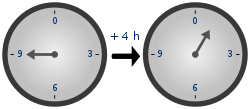 Часы показывают время по модулю 12. n=129+4≡1(mod12){\displaystyle {\begin{aligned}n=12\\9+4&\equiv 1{\pmod {12}}\,\end{aligned}}}.
Часы показывают время по модулю 12. n=129+4≡1(mod12){\displaystyle {\begin{aligned}n=12\\9+4&\equiv 1{\pmod {12}}\,\end{aligned}}}.
В модульной арифметике складывают два целых числа, а полученную сумму делят на целое положительное число, называемое впоследствии модулем. Результатом модульной операции является остаток от деления. Для любого модуля n{\displaystyle n} множество целых чисел от 0{\displaystyle 0} до n−1{\displaystyle n-1} образует группу по сложению. Обратным
элементом к a{\displaystyle a} является число a−1=n−a{\displaystyle a^{-1}=n-a}, нейтральный элемент — 0{\displaystyle 0}. Наглядным примером такой группы
могут быть часы с циферблатом[11].
Применение теории групп не ограничивается только математикой, её широко используют в таких науках как физика, химия и информатика.
- Целые числа с операцией сложения. (Z,+){\displaystyle (\mathbb {Z} ,+)} — коммутативная группа с нейтральным элементом 0{\displaystyle 0}. Целые числа с операцией умножения не будут образовывать группу. Замкнутость, ассоциативность и существование нейтрального элемента будет иметь место, но не выполнится аксиома о существовании обратного элемента. Например, a=2{\displaystyle a=2}, тогда a⋅b=1{\displaystyle a\cdot b=1} то есть b=1/2{\displaystyle b=1/2}. Обратный элемент не является целым числом[12].
- Положительные рациональные числа с операцией умножения. Произведение рациональных чисел — снова рациональное число, обратный элемент к рациональному числу представляется обратной дробью, имеется ассоциативность, а нейтральным элементом является единица[12].
- Свободная группа с двумя образующими (F2{\displaystyle F_{2}}) состоит из пустого слова (единица группы) и всех конечных слов из четырёх символов a{\displaystyle a}, a−1{\displaystyle a^{-1}}, b{\displaystyle b} и b−1{\displaystyle b^{-1}} таких, что a{\displaystyle a} не появляется рядом с a−1{\displaystyle a^{-1}} и b{\displaystyle b} не появляется рядом с b−1{\displaystyle b^{-1}}. Операция умножения таких слов — это просто соединение двух слов в одно с последующим сокращением пар aa−1{\displaystyle aa^{-1}}, a−1a{\displaystyle a^{-1}a}, bb−1{\displaystyle bb^{-1}} и b−1b{\displaystyle b^{-1}b}[13].
- Симметрическая группа. Множество всех биекций конечного множества в себя с операцией композиции является конечной группой, которая называется симметрической группой, или группой перестановок. Мощность конечной симметрической группы Sn{\displaystyle S_{n}} для множества из n{\displaystyle n} элементов равна n!{\displaystyle n!}. При n≥3{\displaystyle n\geq 3} эта группа не является абелевой[14]. Любая конечная группа является подгруппой некоторой симметрической группы (теорема Кэли)[12][15].
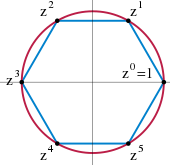 6 комплексных корней из единицы образуют циклическую группу
6 комплексных корней из единицы образуют циклическую группу
- 31≡3(mod5)32≡4(mod5)33≡2(mod5)34≡1(mod5){\displaystyle {\begin{aligned}3^{1}&\equiv 3{\pmod {5}}\\3^{2}&\equiv 4{\pmod {5}}\\3^{3}&\equiv 2{\pmod {5}}\\3^{4}&\equiv 1{\pmod {5}}\,\end{aligned}}}
- Группа кубика Рубика — подгруппа симметрической группы S48{\displaystyle S_{48}}, элементы которой соответствуют преобразованиям кубика Рубика. Композиция двух преобразований снова является преобразованием, для каждого преобразования существует обратный элемент, имеется ассоциативность и нейтральный элемент[17].
- Группы Галуа. Были введены в математику для решения полиномиальных уравнений с помощью свойств симметрии. Например, решение квадратного уравнения ax2+bx+c=0{\displaystyle ax^{2}+bx+c=0} даёт корни: x=−b±b2−4ac2a.{\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.} Подобная формула есть для уравнения третьей и четвёртой степени, но не существует для полиномиального уравнения степени 5{\displaystyle 5} и выше[18].
Классификация простых конечных групп — Википедия
Теорема о классификации простых конечных групп — теорема теории групп, классифицирующая с точностью до изоморфизма простые конечные группы.
Простые конечные группы — «элементарные кирпичики», из которых можно построить любую конечную группу, так же, как любое натуральное число можно разложить в произведение простых. Теорема Жордана — Гёльдера является более точным способом выражения этого факта для конечных групп. Однако существенное отличие от факторизации целых чисел заключается в том, что такие «кирпичики» не будут определять группу однозначно, так как может существовать множество неизоморфных групп с теми же композиционными рядами[en].
Теорема считается доказанной в серии работ примерно 100 авторов, опубликованных в основном с 1955 по 2004 годы и содержащих в общей сложности тысячи страниц текста. Ричард Лайонс[en], Рональд Соломон[en] и (ранее) Дэниел Горенстейн[en] постепенно публикуют упрощённую и пересмотренную версию доказательства.
Теорема классификации находит применение во многих областях математики, так как вопросы о структуре конечных групп (и их действия на другие математические объекты) могут быть иногда сведены к вопросам о конечных простых группах. Благодаря теореме о классификации на такие вопросы можно иногда ответить, проверив каждое семейство простых групп и каждую спорадическую группу.
Теорема: Любая конечная простая группа изоморфна либо одной из 26 спорадических групп, либо принадлежит одному из следующих трёх семейств:
- циклические группы Zp{\displaystyle \mathbb {Z} _{p}} простого порядка;
- знакопеременные группы An{\displaystyle A_{n}} перестановок не менее 5 элементов;
- простые группы типа Ли, а именно:
- классические группы Ли над конечным полем, а именно, группы Шевалле PSL(n,Fq){\displaystyle PSL(n,F_{q})}, PSU(n,Fq){\displaystyle PSU(n,F_{q})}, PSp(n,Fq){\displaystyle PSp(n,F_{q})} и PSO(n,Fq){\displaystyle PSO(n,F_{q})};
- исключительные и скрученные формы групп типа Ли (включая группу Титса).
Обзор доказательства теоремы классификации[править | править код]
Горенстейн[1][2] написал двухтомник с набросками доказательства для низких рангов и нечётных характеристик, а Ашбахер[3] написал 3-й том, покрывающий оставшиеся случаи характеристики 2. Доказательство можно разбить на несколько основных частей:
Группы малого 2-ранга[править | править код]
Простые группы низкого 2-ранга являются, в основном, группами лиева типа с малым рангом над полями нечётной характеристики, наряду с пятью знакопеременными группами, семью группами характеристического типа 2 и девятью спорадическими группами.
Простые группы малого 2-ранга включают:
- Группы 2-ранга 0, другими словами, группы нечётного порядка, которые все являются разрешимыми по теореме Томпсона — Фейта[en]*.
- Группы 2-ранга 1. Силовские 2-подгруппы являются либо циклическими, с которыми легко работать с использованием функций перехода, либо обобщёнными кватернионами, с которыми работают при помощи теоремы Брауэра — Судзуки[en]. В частности, не существует простых групп 2-ранга 1.
- Группы 2-ранга 2. Альперин показал, что силовская подгруппа должна быть диэдральной, квазидиэдральной, сплетённой или силовской 2-подгруппой группы U3(4). Первый случай покрывает теорема Горенстейна — Уолтера, которая показывает, что только простые группы изоморфны L2(q) для нечётных q, или группе A7. Второй и третий случаи покрывает теорема Альперина — Брауэра — Горенстейна, из которой вытекает, что только простые группы изоморфны L3(q){\displaystyle L_{3}(q)} или U3(q){\displaystyle U_{3}(q)} для нечётных q, или группе M11. Последний случай покрывает Лайонс, показавший, что U3(4){\displaystyle U_{3}(4)} является единственной простой возможностью.
- Группы секционного 2-ранга, не превосходящего 4, классифицируются теоремой Горенстейна – Харады[en].
Классификация групп малого 2-ранга, особенно рангов, не превосходящих 2, интенсивно использует обычную и модулярную теорию характеров, которая почти нигде не применяется явно в других местах классификации.
Все группы за пределами малых 2-рангов можно разбить на два больших класса — группы компонентного типа и группы характеристического типа 2. Если группа имеет секционный 2-ранг, не меньший 5, МакВильямс показал, что её силовские 2-подгруппы связны, а из теоремы баланса[en] следует, что любая простая группа со связной силовской 2-подгруппой либо является группой компонентного типа, либо группой характеристического типа 2. (Для групп низкого 2-ранга доказательство этого не проходит, поскольку теоремы, такие как теорема о сигнализаторном функторе[en], работают только для групп с элементарными абелевыми подгруппами ранга по меньшей мере 3.)
Группы компонентного типа[править | править код]
Говорят, что группа является группой компонентного типа, если для некоторого централизатора C инволюции C/O(C) имеет компоненту (квазипростую субнормальную подгруппу; здесь O(C) — ядро C, максимальная нормальная подгруппа нечётного порядка).
Они представлены в основном группами лиева типа нечётной характеристики с большим рангом и знакопеременными группами, а также некоторыми спорадическими группами.
Главный шаг в данном случае — исключить препятствие с ядром инволюции. Делается это с помощью B-теоремы[en], которая утверждает, что любая компонента C/O(C) является образом компоненты ядра C.
Идея заключается в том, что эти группы имеют централизатор инволюции с компонентой, являющейся меньшей квазипростой группой, которая может считаться уже известной по индукции. Так что для классификации этих групп можно взять каждое центральное расширение каждой известной конечной простой группы и найти все простые группы с централизатором инволюции с этой группой в качестве компоненты. Это даёт огромное число различных случаев, требующих проверки — помимо того, что имеются 26 спорадических групп, 16 семейств групп лиева типа и знакопеременные группы, ещё и многие группы малого ранга или над малыми полями ведут себя отлично от основного случая и должны быть рассмотрены отдельно. Кроме того, группы лиева типа чётной и нечётной характеристики также ведут себя по-разному.
Группы характеристического типа 2[править | править код]
Группа имеет характеристический тип 2, если обобщённая группа Фиттинга[en] F*(Y) любой 2-локальной подгруппы Y является 2-группой. Как подсказывает название, эти группы, грубо говоря, являются группами лиева типа над полями характеристики 2, плюс некоторое количество других групп, знакопеременных, спорадических или нечётной характеристики. Классификация этих групп делится на случаи большого и малого ранга, где ранг — наибольший ранг нечётной абелевой подгруппы, нормализующей нетривиальную 2-подгруппу, и этот ранг часто (но не всегда) является рангом подалгебры Картана, когда группа является группой лиева типа характеристики 2.
Группы ранга 1 — это тонкие группы, классифицированные Ашбахером, а группы ранга 2 — это доставившие немало проблем квазитонкие группы[en], классифицированные Ашбахером и Смитом. Они, грубо говоря, соответствуют группам лиева типа рангов 1 или 2 над полями характеристики 2.
Группы ранга 3 и выше делятся на три класса согласно теореме о трихотомии[en], доказанной Ашбахером для ранга 3 и Горенстейном с Лайонсом для ранга 4 и выше.
Эти три класса: группы типа GF(2) (в основном классифицированные Тиммесфельдом), группы «стандартного типа» для некоторых нечётных простых (классифицированы теоремой Гилмана — Гриса и работами некоторых других авторов) и группы «уникального» (uniqueness) типа, для которых из результата Ашбахера вытекает, что среди них нет простых групп.
Случай общего высокого ранга представляют большей частью группы лиева типа над полями характеристики 2 с рангом по меньшей мере 3 или 4.
Существование и единственность простых групп[править | править код]
Большая часть классификации даёт описание каждой простой группы. Необходимо проверить, что существует простая группа для каждого описанного случая и что она единственна. Это даёт большое число дополнительных проблем. Например, оригинальные доказательства существования и единственности Монстра занимают около 200 страниц, а идентификация групп Ри Томпсоном и Бомбиери была одной из труднейших частей классификации. Многие из доказательств существования и некоторые из доказательств единственности для спорадических групп первоначально использовали компьютерные вычисления, большинство из которых затем были заменены более короткими доказательствами, сделанными вручную.
Программа Горенстейна[править | править код]
В 1972 году Горенстейн[4] объявил программу завершения классификации конечных простых групп, состоящую из следующих 16 шагов:
- Группы низкого 2-ранга. По существу, это было сделано Горенстейном и Харадой, которые классифицировали группы с секционным 2-рангом, не превосходящим 4. Большинство случаев 2-ранга, не превосходящего 2, уже было сделано к тому времени Горенстейном, объявившим программу.
- Полупростота 2-слоёв. Задача заключается в доказательстве, что 2-слой централизатора инволюции в простой группе является полупростым.
- Стандартная форма при нечётной характеристике. Если группа имеет инволюцию с 2-компонентой, являющейся группой лиева типа с нечётной характеристикой, нужно показать, что группа имеет централизатор инволюции в «стандартной форме», что означает, что централизатор инволюции имеет компоненту лиева типа с нечётной характеристикой и имеет централизатор с 2-рангом 1.
- Классификация групп нечётного типа. Задача заключается в доказательстве, что если группа имеет централизатор инволюции в «стандартной форме», то эта группа является группой лиева типа с нечётной характеристикой. Задачу решил Ашбахер, доказав классическую теорему об инволюции[en].
- Квазистандартная форма
- Центральные инволюции
- Классификация знакопеременных групп
- Некоторые спорадические группы
- Тонкие группы. Простые тонкие конечные группы с 2-локальным p-рангом, не превосходящим 1 для нечётных простых p, классифицировал Ашбахер в 1978
- Группы со строго p-вложенной подгруппой для нечётных p
- Метод сигнализаторного функтора для нечётных простых чисел. Главная задача — доказать теорему о сигнализаторном функторе[en] для неразрешимых сигнализаторных функторов. Задачу решил Макбрайд в 1982.
- Группы характеристического типа p. Это задача о группах со строго p-вложенной 2-локальной подгруппой для нечётного p, которую решил Ашбахер.
- Квазитонкие группы. Квазитонкая группа[en] — это группа, 2-локальные подгруппы которой имеют p-ранг, не превосходящий 2, для всех нечётных простых p. Задача заключается в классификации таких простых групп с характеристическим типом 2. Задачу выполнили Ашбахер и Смит в 2004 году.
- Группы низкого 2-локального 3-ранга. Задача была, по существу, уже решена теоремой о трихотомии[en] Ашбахера для групп с e(G)=3. Главное изменение заключалось в замене 2-локального 3-ранга на 2-локальный p-ранг для нечётных простых чисел.
- Централизаторы 3-элементов в стандартной форме. Задача, по существу, решена теоремой о трихотомии[en].
- Классификация простых групп с характеристическим типом 2. Эта часть классификации была выполнена с помощью теоремы Гилмана — Гриса[en], в которой 3-элементы были заменены на p-элементы для нечётных простых чисел.
Горенстейн объявил в 1983 году, что все конечные простые группы классифицированы, но заявление было преждевременным, так как он был недостаточно осведомлён относительно классификации квазитонких групп[en]. Об окончательном завершении доказательства объявил Ашбахер[5] в 2004 году после того, как он вместе со Смитом опубликовал 1221-страничное доказательство для недостававшего квазитонкого случая.
Хронология доказательства[править | править код]
Большая часть информации в списке взята из статьи Соломона[6]. Приведённые даты, как правило, являются датой публикации полного доказательства результата. Эта дата иногда на несколько лет позже доказательства или первого объявления результата, так что может показаться, что события идут в «неверном» порядке.
| Дата публикации | |
|---|---|
| 1832 | Галуа вводит нормальные подгруппы и находит простые группы An (n⩾5{\displaystyle n\geqslant 5}) и PSL2(Fp) (p⩾5{\displaystyle p\geqslant 5}) |
| 1854 | Кэли определяет абстрактные группы |
| 1861 | Матьё описывает первые две группы Матьё M11, M12, первые спорадические простые группы, и объявляет о существовании группы M24. |
| 1870 | Жордан перечисляет некоторые простые группы — знакопеременные и проективные специальные линейные группы, и подчёркивает важность этих простых групп. |
| 1872 | Сюлов доказывает Теоремы Силова |
| 1873 | Матьё вводит ещё три группы Матьё M22, M23, M24. |
| 1892 | Отто Гёльдер доказывает, что порядок любой неабелевой конечной простой группы должен быть произведением по меньшей мере четырёх (не обязательно различных) простых чисел и ставит вопрос о классификации конечных простых групп. |
| 1893 | Коул классифицирует простые группы с порядком до 660 |
| 1896 | Фробениус и Бёрнсайд начали изучение теории характеров конечных групп. |
| 1899 | Бёрнсайд классифицирует простые группы, в которых централизатор любой инволюции является нетривиальной элементарной абелевой 2-группой. |
| 1901 | Фробениус доказывает, что группа Фробениуса[en] имеет ядро Фробениуса, так что она не является простой. |
| 1901 | Леонард Диксон определяет классические группы над произвольными конечными полями и исключительные группы типа G2 над полями с нечётной характеристикой. |
| 1901 | Диксон вводит исключительные конечные простые группы типа E6. |
| 1904 | Бёрнсайд использует теорию характеров для доказательства теоремы Бёрнсайда, что порядок любой неабелевой простой группы должен делиться по меньшей мере на 3 различных простых числа. |
| 1905 | Диксон вводит простые группы типа G2 над полями с чётной характеристикой |
| 1911 | Бёрнсайд высказывает гипотезу, что любая неабелева конечная простая группа имеет чётный порядок |
| 1928 | Холл доказывает существование подгрупп Холла[en] разрешимых групп |
| 1933 | Холл начинает изучение p-групп |
| 1935 | Брауэр начинает изучение модулярных характеров[en] |
| 1936 | Цассенхаус[en] классифицирует конечные строго 3-транзитивные группы перестановок |
| 1938 | Фиттинг[en] вводит подгруппу Фиттинга[en] и доказывает теорему Фиттинга, что для разрешимых групп подгруппа Фиттинга содержит централизатор группы. |
| 1942 | Брауэр описывает p-модулярные характеры групп, порядок которых делится на p, но не на p2. |
| 1954 | Брауэр классифицирует простые группы с централизатором инволюции GL2(Fq). |
| 1955 | Из теоремы Брауэра — Фаулера[en] следует, что число конечных простых групп с заданным централизатором инволюции конечно, что даёт повод для попытки классификации с использованием централизаторов инволюций. |
| 1955 | Шевалле вводит группы Шевалле, в частности, исключительные простые группы типов F4, E7 и E8. |
| 1956 | Теорема Холла — Хигмана[en] |
| 1957 | Судзуки показал, что все конечные простые CA-группы нечётного порядка цикличны. |
| 1958 | Теоерма Брауэра — Судзуки — Уолла[en] описывает проективные специальные линейные группы ранга 1 и классифицирует простые CA-группы. |
| 1959 | Штейнберг ввёл группы Штейнберга, что дало новые конечные простые группы типов 3D4 и 2E6 (вторую из них почти в то же время нашёл независимо Жак Титс). |
| 1959 | Теорема Брауэра — Судзуки[en] о группах с обобщёнными кватернионными силовскими 2-подгруппами показала, что среди них нет простых групп. |
| 1960 | Томпсон доказал, что группа с автоморфизмами без неподвижных точек простого порядка нильпотентна. |
| 1960 | Фейт, Холл и Томпсон показывают, что все конечные простые CN-группы[en] нечётного порядка цикличны. |
| 1960 | Судзуки вводит группы Судзуки[en] типа 2B2. |
| 1961 | Ри вводит группы Ри типа 2F4 и 2G2. |
| 1963 | Фейт и Томпсон доказали теорему о нечётном порядке[en]*. |
| 1964 | Титс вводит BN-пары для групп лиева типа и находит группу Титса |
| 1965 | Теорема Горенстейна — Уолтера[en] классифицирует группы с диэдральными силовскими 2-подгруппами. |
| 1966 | Глауберман доказывает Z*-теорему[en] |
| 1966 | Янко вводит группу Янко J1[en], первую новую спорадическую группу почти за столетие. |
| 1968 | Глауберман доказывает ZJ-теорему[en] |
| 1968 | Хигман и Симс вводят группу Хигмана — Симса[en] |
| 1968 | Конвей вводит группы Конвея[en]* |
| 1969 | Теорема Уолтера[en] классифицирует группы с абелевыми силовскими 2-подгруппами |
| 1969 | Появление спорадической группы Судзуки[en], группы Янко J2, группы Янко J3[en], группы МакЛафлина[en] и группы Хельда[en]. |
| 1969 | Горенстейн вводит сигнализаторные функторы[en], основываясь на идеях Томпсона. |
| 1970 | МакВильямс показал, что 2-группы без нормальных абелевых подгрупп ранга 3 имеют секционный 2-ранг, не превосходящий 4. (Простые группы с силовскими подгруппами, удовлетворяющие последнему условию, позже классифицировали Горенстейн и Харада.) |
| 1970 | Бендер вводит подгруппу Фиттинга[en] |
| 1970 | Теорема Альперина — Брауэра — Горенстейна[en] классифицирует группы с квазидиэдральными или скрученными силовскими 2-подгруппами, завершая тем самым классификацию простых групп с 2-рангом, не превосходящим 2 |
| 1971 | Фишер вводит три группы Фишера |
| 1971 | Томпсон классифицирует квадратичные пары[en] |
| 1971 | Бендер классифицирует группы с сильно вложенной подгруппой[en] |
| 1972 | Горенстейн предлагает 16-этапную программу классификации конечных простых групп. |
| 1972 | Лайонс вводит группу Лайонса[en] |
| 1973 | Рудвалис представляет группу Рудвалиса |
| 1973 | Фишер открывает группу «Малый Монстр»[en] (работа не опубликована), которую Фишер и Грисс используют для открытия группы «Монстр», которая, в свою очередь, приводит к обнаружению Томпсоном cпорадической группы Томпсона[en] и Нортоном группы Харады-Нортона[en] (также найдена другим способом Харадой). |
| 1974 | Томпсон классифицирует N-группы[en]* — группы, в которых все локальные подгруппы разрешимы. |
| 1974 | Теорема Горенстейна — Харады[en] классифицирует простые группы, секционные 2-ранги которых не превосходят 4, деля тем самым оставшиеся конечные простые группы на группы компонентного типа и группы характеристического типа 2. |
| 1974 | Титс показывает, что группы с парами (B, N) ранга, не меньшего 3, являются группами лиева типа |
| 1974 | Ашбахер классифицирует группы с подходящим 2-порождённым ядром[en] |
| 1975 | Горенстейн и Уолтер доказывают теорему о L-балансе[en] |
| 1976 | Глауберман доказывает теорему о разрешимом сигнализаторном функторе[en] |
| 1976 | Ашбахер доказывает теорему о компонентах[en], показывая, что группы нечётного типа, удовлетворяющие некоторым условиям, имеют компоненту в стандартной форме. Группы с компонентой в стандартной форме были классифицированы в большой совокупности статей различных авторов. |
| 1976 | О’Нан вводит группу О’Нана[en] |
| 1976 | Янко вводит группу Янко J4[en], последнюю открытую спорадическую группу |
| 1977 | Ашбахер описывает группы лиева типа с нечётной характеристикой в своей классической теореме об инволюции[en]. После этой теоремы, которая, в некотором смысле, имеет дело с «большинством» простых групп, наступило чувство, что конец классификации не за горами. |
| 1978 | Тиммесфельд разбивает классификацию групп типа GF(2)[en] на несколько меньших задач. |
| 1978 | Ашбахер классифицирует тонкие конечные группы, которые, главным образом, являются группами лиева типа с рангом 1 над полем чётной характеристики. |
| 1981 | Бомбиери использует теорию исключения для завершения работы Томпсона по описанию групп Ри, одного из самых трудных шагов классификации. |
| 1982 | Макбрайд доказывает теорему о сигнализаторном функторе[en] для всех конечных групп. |
| 1982 | Грисс строит группу «Монстр» вручную |
| 1983 | Теорема Гилмана — Гриса[en] классифицирует группы характеристического типа 2 и ранга по меньшей мере 4 со стандартными компонентами, одним из трёх случаев теоремы о трихотомии. |
| 1983 | Ашбахер доказывает, что никакая конечная группа не удовлетворяет гипотезе уникальности[en], одному из трёх случаев теоремы о трихотомии для групп характеристического типа 2. |
| 1983 | Горенстейн и Лайонс доказывают теорему о трихотомии[en] для групп характеристического типа 2 и ранга, не меньшего 4, в то время как Ашбахер доказывает её для ранга 3. Это делит такие группы на 3 подкласса — случай уникальности, группы типа GF(2) и группы со стандартными компонентами. |
| 1983 | Горенстейн объявляет о завершении доказательства теоремы классификации. Несколько преждевременно, поскольку доказательство для квазитонкого случая не завершено. |
| 1994 | Горенстейн, Лайонс и Соломон начинают публикацию пересмотренной классификации |
| 2004 | Ашбахер и Смит публикуют работу о квазитонких группах[en] (которые являются, главным образом, группами лиева типа ранга 2 и выше над полями с чётной характеристикой), заполняя последний пробел в классификации, известный на то время. |
| 2008 | Харада и Соломон заполняют небольшой пробел в классификации описанием групп со стандартной компонентой, которая покрывает группу Матьё M22[en]. Этот случай был случайно пропущен в доказательстве классификации ввиду ошибки при вычислении мультипликатора Шура для M22. |
| 2012 | Джорджс Гонтир[en] с соавторами объявил о проверенной на компьютере версии теоремы Томпсона — Фейта[en]*, для чего была использована система автоматического доказательства[en] Coq[7]. |
Доказательство теоремы на момент примерно 1985 года можно назвать первым поколением. Ввиду крайне большой длины доказательства первого поколения и разрозненности входящих в него материалов ведётся большая работа по созданию единого и более простого доказательства, названного доказательством классификации второго поколения; это направление также известно как «ревизионизм». Эту работу ведут Дэниел Горенстейн[en] (до его смерти в 1992 году), Ричард Лайонс и Рональд Соломон. Они выпускают доказательство в виде серии книг, иногда называемой GLS по фамилиям авторов.
К 2018 году готово восемь томов GLS[⇨]; планируется, что последний, 12-й том выйдет в 2023 году[8]. Хотя доказательство второго поколения более компактное, чем доказательство первого поколения, оно всё равно займёт тысячи страниц.
Помимо книг GLS, в доказательство второго поколения входит двухтомник The classification of quasithin groups Ашбахера и Смита, посвящённый квазитонкому случаю[8].
Горенстейн с соавторами указали причины, по которым можно упростить имеющееся доказательство.
- Наиболее важно, что теперь известно само правильное финальное утверждение теоремы. Теперь могут быть использованы более простые методы, подходящие для известных типов простых конечных групп. Напротив, авторы, работавшие с первым поколением доказательства, не знали, сколько существует спорадических групп, и, фактически, некоторые спорадические группы (такие как группы Янко) были обнаружены во время доказательства других случаев теоремы классификации. В результате многие части теоремы доказывались с использованием слишком общих методов.
- Поскольку окончательное утверждение было неизвестно, первое поколение доказательства состоит из большого числа самостоятельных теорем, имеющих дело с важными особыми случаями. Большая часть работы по доказательству этих теорем посвящена анализу многочисленных особых случаев. В большом, упорядоченном доказательстве работа с многими из этих особых случаев может быть отложена, пока не появится возможность применения более сильных предположений. Цена этой стратегии — некоторые теоремы первого поколения не имеют тогда сравнительно коротких доказательств, а опираются на полную классификацию.
- Многие теоремы первого поколения перекрывают друг друга и тем самым разбивают классификацию на возможные случаи неэффективно. В результате семейства и подсемейства конечных простых групп были идентифицированы неоднократно. Пересмотренное доказательство исключает эти повторения путём другого разбиения на случаи.
- Теоретики конечных групп получили большой опыт в такого рода работе и имеют возможность использовать новые методы.
Ашбахер[5] назвал работу над задачей классификации, проведённую Ульрихом Майрфранкенфельдом, Берндом Штеллмахером, Гернотом Стротом и несколькими другими третьим поколением программы. Одна из целей этой работы — рассматривать все группы в характеристике 2 единообразно с помощью метода соединения.
Почему доказательство так длинно?[править | править код]
Горенстейн обсуждал подходы к поиску гораздо более простого доказательства, наподобие классификации компактных групп Ли[en], и причины, по которым такого доказательство может не существовать вовсе.
- Наиболее очевидная причина — список простых групп достаточно сложен: помимо 26 спорадических групп, имеется много особых случаев, которые необходимо рассмотреть в любом доказательстве. До сих пор не найдено ясное единообразное описание конечных простых групп, подобное параметризации компактных групп Ли с помощью диаграмм Дынкина.
- Атья и другие высказали предположение, что классификация могла бы быть упрощена путём построения некоторого геометрического объекта, на котором группы действуют, а затем классифицировать геометрические структуры этого объекта. Проблема здесь в том, что никто не смог предложить простого пути нахождения такой геометрической структуры, ассоциированной с простой группой. В некотором смысле классификация уже работает путём нахождения геометрических структур, таких как пары (B, N), но они появляются в самом конце очень длинного и трудного анализа структуры конечной простой группы.
- Другое предложение по упрощению доказательства заключается в большем использовании теории представлений. Проблема здесь в том, что теория представлений, по-видимому, требует очень тесного контроля над подгруппами группы, чтобы работать хорошо. Для групп малого ранга такой контроль имеется и теория представлений работает хорошо, но для групп большего ранга никто не добился успеха в использовании теории представлений для упрощения классификации. В начале попыток классификации прилагались большие усилия для использования теории представлений, но это не принесло больших успехов для случаев больших рангов.
В этом разделе перечислены некоторые результаты, которые доказаны с помощью теоремы классификации конечных простых групп.
G₂ — Википедия
Материал из Википедии — свободной энциклопедии
G2 в математике — название трёх простых групп Ли (комплексной, вещественной компактной и вещественной разделённой), связанной с ними алгебры Ли g2{\displaystyle {\mathfrak {g}}_{2}}, а также нескольких алгебраических групп. Являются наименьшими из пяти исключительных простых групп Ли, рангом 2 и размерностью 14, с точными нетривиальными конечномерными линейными представлениями. Всего G2 имеет два фундаментальных представления размерностью 7 и 14, первое из которых отвечает короткому корню системы корней G2.
Компактная форма G2 является группой автоморфизмов алгебры октонионов (октав) или подгруппой группы SO(7), оставляющую на месте фиксированный 8-мерный спинор (в её спинорном представлении).
Существуют 3 простые вещественные алгебры Ли, ассоционированные с данной системой корней:
- Лежащая в основе комплексной алгебры Ли G2 сугубо действительная алгебра Ли 28-мерна и односвязна. Комплексное сопряжение является её внешним автоморфизмом. Максимальная компактная подгруппа ассоциированной с этой алгеброй группы и есть компактная форма G2.
- Алгебра Ли в компактной форме имеет размерность 14. Ассоциированная группа Ли не имеет внешних автоморфизмов, центра и является односвязной и компактной.
- Алгебра Ли в некомпактной (разделённой) форме содержит 14 измерений. Ассоциированная простая группа Ли имеет фундаментальную группу 2 порядка, а её группа внешних автоморфизмов — тривиальная группа. Её максимальная компактная подгруппа — SU(2)×SU(2)/(−1×−1). Для данной группы существует неалгебраическая двойная универсальная накрывающая группа (односвязная).
Схема Дынкина[править | править код]
Система корней G2[править | править код]
Несмотря на то, что корневые векторы можно разместить в 2-мерном пространстве, более симметричным выглядит их выражение тремя координатами, сумма которых равна нулю:
- (1,−1,0), (−1,1,0)
- (1,0,−1), (−1,0,1),
- (0,1,−1), (0,−1,1),
- (2,−1,−1), (−2,1,1),
- (1,−2,1), (−1,2,−1),
- (1,1,−2), (−1,−1,2),
и простые положительные корневые вектора
- (0,1,−1), (1,−2,1).
Группа Вейля/Кокстера[править | править код]
Для алгебры G2 это — группа диэдра D12 12 порядка.
Матрица Картана[править | править код]
- (2−3−12){\displaystyle {\begin{pmatrix}2&-3\\-1&2\end{pmatrix}}}
Специальные голономии[править | править код]
G2 — одна из тех специальных групп, которые могут быть группами голономии римановой метрики. Многообразия, обладающие G2-голономией, называются G2-многообразиями.
Группа периодической системы — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 сентября 2018;
проверки требуют 8 правок.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 21 сентября 2018;
проверки требуют 8 правок.
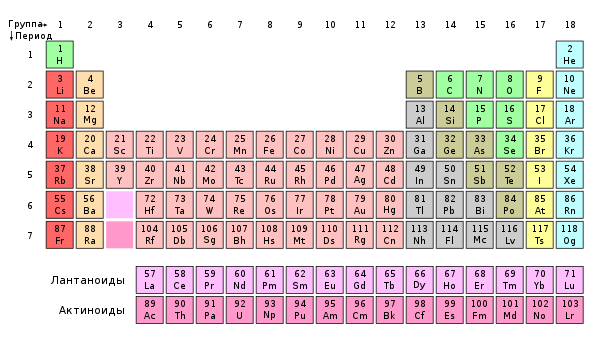
!Гру́ппа периодической системы химических элементов — последовательность атомов по возрастанию заряда ядра, обладающих однотипным электронным строением.
Номер группы определяется количеством электронов на внешней оболочке атома (валентных электронов) и, как правило, соответствует высшей валентности атома.
В короткопериодном варианте периодической системы группы подразделяются на подгруппы — главные (или подгруппы A), начинающиеся с элементов первого и второго периодов, и побочные (подгруппы В), содержащие d-элементы. Подгруппы также имеют названия по элементу с наименьшим зарядом ядра (как правило, по элементу второго периода для главных подгрупп и элементу четвёртого периода для побочных подгрупп). Элементы одной подгруппы обладают сходными химическими свойствами.
С возрастанием заряда ядра у элементов одной группы из-за увеличения числа электронных оболочек увеличиваются атомные радиусы, вследствие чего происходит снижение[источник не указан 1075 дней]электроотрицательности, усиление[источник не указан 1075 дней]металлических и ослабление[источник не указан 1075 дней]неметаллических свойств элементов, усиление восстановительных и ослабление окислительных свойств образуемых ими веществ.
С 1989 года Международным союзом теоретической и прикладной химии (IUPAC) в качестве основного варианта периодической системы утверждена длиннопериодная форма[1]. В связи с этим IUPAC рекомендует сплошную нумерацию групп: арабскими цифрами от 1 до 18.
Несмотря на это, продолжают применяться ставшие традиционными системы нумерации с использованием римских цифр и латинских букв, отличающиеся для Америки и Европы.
Современная система нумерации содержит следующие группы (старые системы, европейская и американская, приведены в скобках):
- Группа 1 (IA, IA): щелочные металлы
- Группа 2 (IIA, IIA): щёлочноземельные металлы
- Группа 3 (IIIB, IIIA): подгруппа скандия
- Группа 4 (IVB, IVA): подгруппа титана
- Группа 5 (VB, VA): подгруппа ванадия
- Группа 6 (VIB, VIA): подгруппа хрома
- Группа 7 (VIIB, VIIA): подгруппа марганца
- Группа 8 (VIIIВ, VIIIA): подгруппа железа
- Группа 9 (VIIIВ, VIIIA): подгруппа кобальта
- Группа 10 (VIIIВ, VIIIA): подгруппа никеля
- Группа 11 (IB, IB): подгруппа меди
- Группа 12 (IIB, IIB): подгруппа цинка
- Группа 13 (IIIA, IIIB): подгруппа бора
- Группа 14 (IVA, IVB): подгруппа углерода
- Группа 15 (VA, VB): подгруппа азота (пниктогены)
- Группа 16 (VIA, VIB): подгруппа кислорода (халькогены)
- Группа 17 (VIIA, VIIB): галогены
- Группа 18 (VIIIA, VIIIB)[2]: инертные газы
- ↑ Сайфуллин Р. С., Сайфуллин А. Р. Новая таблица Менделеева // Химия и жизнь.— 2003.— № 12.— С. 14—17.
- ↑ Подгруппа гелия (инертные газы) иногда, особенно в старых изданиях, обозначается цифрой 0.
