Методы оптимизации производства: Оптимизация процессов производства: методы, задачи и технологии – ТОП: тотальная оптимизация производства — Инструментарий управленца / «Вестник McKinsey»

Содержание

Оптимизация процессов производства: методы, задачи и технологии

Процессы, затрагиваемые оптимизацией

Оптимизация производственных процессов затрагивает основные сферы изготовления продукции на предприятии:

Повышение оборота продукции. В условиях конкурентного рынка повышение объемов продукции редко приводит к желаемому результату, лишь увеличивает затраты предприятия. Необходимо выделить продукт пониженной ценой, дополнительными характеристиками или другими преимуществами для клиентов, чтобы повысить оборот.
Снижение операционных расходов. Оптимизация процессов на предприятии сводится к повышению эффективности работы сотрудников и снижению их численности. Также устраняются неиспользуемые складские помещения, оборудование.
Рациональное распределение запасов предприятия. Снижение количества запасов приводит к промышленному застою, снижению объемов производимой продукции и общей стагнации для бизнеса. В рамках указанных мероприятий необходимо правильно рассчитывать количество и качество запасов. Работа с запасами проводится в комплексе с оборотом.

В результате всех процедур, производительность организации должна возрастать, а финансовые затраты оставаться на прежнем уровне либо уменьшаться.

Методы оптимизации производства

При управлении предприятием в целях оптимизации производственной деятельности, в первую очередь, затрагиваются текущие процессы. Целью специалистов становится улучшение актуальных методов изготовления продукции. Только если оптимизационная деятельность не помогает улучшить состояние компании, используется модернизация оборудования.

Существует несколько основных методов сократить траты и увеличить доходы:

Бережливое производство;
Тотальная оптимизация всех процессов, происходящих в компании.

Задача специалистов заключается в том, чтобы оптимизировать производство на постоянной основе. Временные меры приносят или незначительный, или краткий результат.

Бережливое производство

Данная модель оптимизации подразумевает исключение любых процессов в организации, которые приводят к дополнительным тратам бюджета. Основное условие – изготовление ограниченного количества товаров, использование ограниченного числа сотрудников и т. д. В рамках оптимизации производства продукции и других сфер деятельности, при бережливом методе сокращаются траты на:

Завод не занимается перепроизводством продукции, изготавливает ровно столько, сколько нужно потребителю;
Материалы и сырье, образующиеся между этапами производства готовых изделий больше не хранятся на складах, сокращается производственный цикл;
Изменяется расположение цехов и оборудования так, чтобы затраты на транспортировку материалов больше не требовались;
Закупается дополнительное оборудование, исправляются проектные ошибки, чтобы сократить число циклов при производстве каждой единицы продукции;
Сокращается количество запасов продукции в том случае, если они лежат без конкретной цели продажи;
Минимизируется возможность изготовления бракованной продукции;
Оптимизируется работа персонала, организуется удобное рабочее пространство для скорейшей работы.

Путь бережливого производства дает долгосрочный результат без потери в качестве итоговых товаров. Технология характеризуется ускорением и упрощением рабочих процессов, благодаря чему расходы понижаются естественным образом, а темп производства растет.

Тотальная оптимизация

Принципы тотального метода оптимизации производства отправляют предпринимателя к подчиненным. К процедурам по снижению затрат привлекаются сотрудники. Формируется отдел или нанимаются специалисты в данной области, которые создают проект. На основании проекта можно оптимизировать производство, снизить затраты на покупку сырья и количество брака. Программа подразумевает следующие факторы:

Работники компании знают производственный процесс лучше начальства. Недостатки оборудования, неудобные моменты в работе, неправильное распределение ресурсов – все это влияет на качество и скорость изготовления продукции.
При разработке проекта используется мозговой штурм, на котором во внимание принимаются даже самые безумные идеи. Впоследствии из них могут получиться интересные варианты по снижению расходов компании.
Чтобы сотрудники компании активнее принимали участие в разработке проекта, используется материальное вознаграждение. Из всего коллектива отбирается рабочая группа, которая будет направлять специалистов.
Деятельность рабочей группы отслеживается руководством предприятия. Для выполнения задач оптимизации производства необходим жесткий контроль и сотрудничество всех слоев персонала.

В России уже используется данный вид оптимизации на крупных предприятиях. Обе модели позволяют добиваться значительных результатов в улучшении работы фабрики или другой промышленной компании.

Почему оптимизация не работает

В некоторых случаях оптимизация ресурсов производства не приносит видимых результатов. Тому есть распространенные причины:

Специфика компании не учтена;
Используется только механистический подход;
Не соблюдается этапность мероприятий;
Руководство не контролирует или не исполняет рекомендации.

Компания «Арбор Прайм» предлагает собственных специалистов по оптимизации производственных предприятий, а также всеобъемлющие консультации по данной теме. Оптимизировать и улучшить работу организации поможет только продуманный, системный подход.

Решение задач мониторинга, диагностики и оптимизации производственных процессов

ТОП: тотальная оптимизация производства — Инструментарий управленца / «Вестник McKinsey»

В базовых отраслях промышленности (например, в металлургической, химической, целлюлозно-бумажной, энергетической) управленцы имеют дело с постоянно увеличивающейся сложностью ведения бизнеса. Любая компания в этих отраслях сталкивается с глобальной конкуренцией
на рынке, испытывая все возрастающее давление необходимости снижения затрат. Рассмотрим в качестве примера сталелитейную отрасль. За последние два десятилетия в целом мировая стальная индустрия приносила только 4% возврата на активы. Низкая доходность объясняется
выходом на рынок новых игроков и усилением конкуренции. Стальные компании, в т. ч. лидеры рынка Posco (Южная Корея), China Steel (Тайвань), Techint (Аргентина), выросли и превратились в сильных игроков на развивающихся рынках. Используя новейшие технологии
и низкую себестоимость производства, они предлагают на мировой рынок продукцию высокого качества по минимальной цене. При среднем уровне загрузки производства компаний в развитых странах (Европа, Япония, США), равном 80%, единственным способом остаться на
плаву является постоянное повышение эффективности и сокращение затрат.

Из существующей практики известно много стратегий, методик и способов сокращения затрат, которые компании более или менее успешно применяют. Все эти методы можно свести к трем: директивный, реинжиниринг и «снизу вверх». Директивный подход предполагает сокращение
операционных бюджетов подразделений на определенную величину (10 —20%) в «приказном» порядке. Реинжиниринг заключается в коренном пересмотре основных бизнес–процессов, организации и технологии ведения бизнеса с целью перехода на новый качественный уровень.
Оптимизация затрат «снизу вверх» проводится путем совершенствования большого количества процессов, технологий и методов организации труда на уровне рядовых подразделений, но без изменения основных процессов и структуры бизнеса.

Директивный подход зачастую бывает наиболее эффективным и дает немедленный результат. Вместе с тем основным и очень существенным его недостатком является отсутствие приоритетов, четко увязанных со стратегией. В результате локальное сокращение затрат может
привести к стагнации доходов бизнеса, снижению доли рынка и прибыльности. Наиболее целесообразно применять директивный подход выборочно и только там, где прослеживается очевидная неэффективность (например, большое количество персонала в службе кадров в сравнении
с компаниями–конкурентами).

Реинжиниринг, конечно, можно рассматривать в качестве наиболее эффективного способа снижения затрат и повышения конкурентоспособности компании. Однако большие затраты времени и ресурсов, необходимых для проведения масштабного реинжиниринга основных бизнес–процессов,
могут свести ожидаемый эффект к нулю. Кроме того, основные производственные процессы и технологии, применяемые в базовых отраслях, как правило, уже достаточно отработаны и не имеют потенциала для радикальной оптимизации. Таким образом, компания, решившая провести
реинжиниринг, должна задуматься об одновременном сокращении операционных затрат, чтобы не утратить конкурентных позиций за время реализации этих масштабных перемен.

Сокращение затрат «снизу вверх» является оптимальным способом достижения долгосрочного конкурентного преимущества по затратам при минимальных риске и инвестициях. Принцип осуществления таких программ заключается в вовлечении как можно большего количества
сотрудников в процесс выработки и реализации практических предложений по повышению эффективности, увеличению производительности и улучшению качества на каждом участке производства. Например, в результате реализации идеи закрыть подшипники рольганга прокатного
стана для предотвращения вымывания масла и увеличения срока их службы, предложенной в ходе одного из проектов, экономический эффект составил всего несколько десятков тысяч долларов. Однако несколько сотен таких идей дают ежегодную экономию в десятки миллионов
долларов. Большинство подобных идей «лежит на поверхности». Буквально каждая из компаний имеет огромный потенциал для повышения эффективности и сокращения затрат. Так в чем же дело? Почему он не используется? На наш взгляд, основная причина упущенных возможностей
и стремления руководства применить директивный подход к сокращению затрат заключается в сложности организации системного и структурированного процесса снижения затрат, направленного на мобилизацию компании по пути изменений.

McKinsey столкнулась с этой проблемой несколько десятилетий назад в своей работе с клиентами. В результате была разработана методология организации и проведения масштабных проектов сокращения затрат «снизу вверх» в больших организациях. Эту программу назвали
ТОП — тотальной оптимизацией производства. Программа ТОП разработана на базе опыта лучших мировых компаний, она постоянно совершенствуется. Анализ эффективности программы ТОП в областях электроники, цветной и черной металлургии, горнодобывающей и целлюлозно–бумажной
промышленности показал, что среднее сокращение общих затрат компании после реализации программы составляет 16% (рис. 1).

Цели и задачи программы ТОП

Как уже говорилось, основной целью программы ТОП является оптимизация всех видов деятельности предприятия для повышения эффективности производства. Программа имеет две основные задачи. Первая задача — единовременное и существенное (40% от сокращаемых затрат)
повышение эффективности, которое должно быть достигнуто в кратчайшие сроки. В ходе реализации этой задачи путем тщательного анализа ликвидируется большинство существующих пробелов в деятельности компании. Причем здесь важно не только достичь сокращения затрат,
но и продемонстрировать преимущества программы для внутрикорпоративной деятельности, убедить сотрудников в необходимости преобразований, создать механизмы мотивации и контроля за достижением результата.

Вторая задача программы — создание внутри организации функций и механизмов, способных поддержать процесс преобразований в рамках программы ТОП, превратить его в постоянный, эффективно работающий механизм, призванный обеспечить долговременное преимущество
компании по затратам.

Мировой опыт проведения программ ТОП во всем мире доказал, что улучшений можно достичь одновременно по нескольким параметрам (рис. 2). Примерно 70% целей по сокращению затрат достигается в первые 18 месяцев с начала реализации проекта, а срок окупаемости
требуемых инвестиций не превышает одного года (рис. 3, 4).

Кроме конкретных финансовых результатов, программа ТОП имеет и другие положительные моменты. Так, в ходе реализации проекта составляется полное описание функций производственных и непроизводственных служб, что может служить основой для планирования численности
персонала и разработки долговременных планов развития. В результате реализации программы менталитет сотрудников претерпевает изменения:появляется нацеленность на постоянный контроль и сокращение затрат. Как следствие, повышается качество продукции и услуг,
производительность труда, уровень безопасности и экологичности производства.

Методология программы ТОП

Методология программы ТОП существенно отличается от методологий, традиционно применяемых в программах повышения эффективности:она нацелена не только на повышение эффективности производства, но и на изменение мотивации и эффективности работы самих сотрудников.
Тем самым инициируется долгосрочная программа улучшений. Рассмотрим основные элементы методологии.

Комплексный подход. Цель сокращения затрат ставится в комплексе с целями увеличения производительности, улучшения качества продукции и услуг. Экономический эффект, как правило, достигается за счет «расшивки» узких мест и получения дополнительных
доходов в связи с заменой менее качественной продукции на более качественную. Например, при проведении программы ТОП в упаковочном цеху одной металлургической компании предложение по замене типа используемых подъемных механизмов по перемещению рулонов стального
листа позволило на 80% сократить повреждения краев рулонов и тем самым повысить качество конечной продукции. В результате, компания получила возможность привлечь новых, более требовательных к качеству клиентов, увеличить объем производства и прибыль.

Конкретные цели сокращения затрат, базирующиеся на анализе показателей лучших компаний в отрасли. В начале реализации программы ТОП всем подразделениям ставится цель снизить затраты на 40% от указанных в бюджете. Бюджет сокращаемых затрат
рассчитывается для каждого подразделения исходя из специфики деятельности. Например, для производства 1 т слябов необходимо затратить минимум 1 т стали, которая считается несокращаемой;в то же время отходы, возникающие при превращении стали в слябы, считаются
сокращаемыми. Если же определить долю несокращаемых затрат не представляется возможным, целевые показатели устанавливаются на уровне лучших компаний в отрасли. В среднем 40% сокращаемых затрат равнозначно 15 —20% всех затрат. Данные цели, безусловно, являются
агрессивными, особенно если учесть, что они должны быть выполнены без каких-либо существенных инвестиций. Тем не менее они абсолютно реальны, и это было подтверждено практикой реализации программы ТОП во многих странах, в том числе и в России. Если подразделение
решает поставленные задачи, то по своей эффективности оно выходит на уровень, опережающий наиболее успешных конкурентов.

Использование существующего ноу-хау. Руководители единиц (начальники цехов, участков) несут основную ответственность за организацию и продвижение программы ТОП. Как правило, они четко представляют, где в их подразделениях существует потенциал
повышения эффективности и как его можно реализовать. Кроме того, руководителям легче мотивировать и вовлекать в процесс всех своих сотрудников. Вовлечение в процесс ТОП клиентов этих подразделений, а также смежников позволяет корректно оценить экономический
эффект от реализации идей. То, что при реализации программы используются идеи, исходящие от сотрудников, рождает чувство сопричастности к изменению жизни компании. А это, в свою очередь, приводит к изменению корпоративного менталитета и способствует созданию
системы постоянных, долгосрочных изменений.

Использование нетрадиционных идей. Входе реализации программы под сомнение ставится все, даже абсолютно непоколебимые истины. При этом ориентиром являются лучшие из существующих в мире технологий и практика работы лучших компаний. Так, например,
в ходе реализации одного из предложений количество циклов использования емкостей для сбора шлака на металлургическом заводе было увеличено в 10 раз в сравнении с существовавшей практикой — результат, который казался вначале невероятным, стал возможным за счет
применения современной методики напыления емкостей жаропрочным составом. Четкое отслеживание результатов. Все принятые предложения становятся планами конкретных действий со сроками реализации и конкретным измеримым результатом (например, снижение бюджета подразделения
на закупку сырья и материалов, электроэнергию и т.д.). Для отслеживания хода выполнения этих планов создается специальная, независимая группа контроллинга, которая наделяется широкими полномочиями и имеет возможность контактировать с высшим руководством. Одной
из самых сложных задач, решаемой группой контроллинга, является задача выделения экономического эффекта от реализации программы ТОП от всех прочих изменений в бюджетах и себестоимости, вызванных колебаниями валютного курса, цен на сырье и материалы, реконфигурации
производства, реализации инвестиционных программ.

Четкое отслеживание результатов. Все принятые предложения становятся планами конкретных действий со сроками реализации и конкретным измеримым результатом (например, снижение бюджета подразделения на закупку сырья и материалов, электроэнергию
и т.д.). Для отслеживания хода выполнения этих планов создается специальная, независимая группа контроллинга, которая наделяется широкими полномочиями и имеет возможность контактировать с высшим руководством. Одной из самых сложных задач, решаемой группой
контроллинга, является задача выделения экономического эффекта от реализации программы ТОП от всех прочих изменений в бюджетах и себестоимости, вызванных колебаниями валютного курса, цен на сырье и материалы, реконфигурации производства, реализации инвестиционных
программ.

Процесс программы ТОП

Процесс программы ТОП состоит из последовательно повторяющихся циклов, или «волн», каждая из которых охватывает несколько подразделений (цехов) компании. Количество «волн» определяется размером компании и объемом задействованных ресурсов. Например, в одной
из крупнейших российских металлургических компаний процесс ТОП был осуществлен в 4 «волны» продолжительностью 3 месяца каждая. Эти «волны» состояли из 6 этапов: организация, установка целей, выработка предложений, оценка предложений, подготовка внедрения и
внедрение (рис. 5).

ЭТАП 1. ОРГАНИЗАЦИЯ. Организация процесса ТОП является ее важнейшим этапом, в ходе которого определяются производственные единицы, назначаются их руководители и члены рабочей группы, проводится обучение всех участников процесса. Производственными
единицами могут являться как отдельные небольшие цеха, так и участки более крупных цехов. Количество сотрудников в единице, как правило, не превышает 300 человек. Руководителями единиц назначаются руководители цехов и участков или их заместители. Основными
критериями их отбора являются желание участвовать в программе, отношение к ним коллектива, уровень профессиональной подготовки, общий интеллектуальный уровень. Основой мотивации руководителей единиц выступает возможность реализации идей, не осуществленных
до этого по разным причинам, а также проявить себя перед высшим руководством и коллективом. Руководители единиц несут основную ответственность за сокращение затрат. Они отвечают за выработку предложений, расчет экономического эффекта и представление идей на
утверждение высшему руководству. Типовая организация программы ТОП представлена на рис. 6.

ЭТАП 2. УСТАНОВКА ЦЕЛЕЙ. Основной задачей этого этапа является установка конкретных и обоснованных целей сокращения затрат. Для этого сначала рассчитывается общий бюджет производственной единицы. Чтобы упростить эту задачу, при формировании
единиц следует придерживаться существующего организационного разделения и структуры финансового учета. После определения бюджета единицы составляется схема основных производственных процессов, а также потоков сырья и материалов. Затраты единицы распределяются
между бизнес–процессами, определяется примерная стоимость каждого процесса.

Затем затраты подразделяются на операционные и технические (сырье, энергия) и определяются несокращаемые затраты и затраты, не рассматриваемые в проекте (например, амортизация). В категорию несокращаемых, как правило, попадает часть затрат на сырье и энергию.
При этом уровень несокращаемых затрат определяется путем теоретического расчета минимальной потребности (т. е. рассчитывается минимально возможный уровень потребления сырья и энергии при условии нулевых отходов, утечек и пр.). Все остальные затраты (на персонал,
ремонты, накладные, административные расходы, запасные части) считаются полностью сокращаемыми. Типичный пример разбивки расходов подразделения на сокращаемые и несокращаемые представлен на рис. 7. После того как определены бюджеты подразделений и уровень
несокращаемых расходов, производственным единицам ставится цель сокращения оставшейся части бюджета на 40%. Это означает, что руководитель единицы и рабочая группа должны выработать и экономически обосновать предложения, суммарный эффект от реализации которых
в течение «волны» составит минимум 40% сокращаемого бюджета единицы.

ЭТАП 3. ВЫРАБОТКА ПРЕДЛОЖЕНИЙ ПО СОКРАЩЕНИЮ ЗАТРАТ. Основным механизмом выработки идей по сокращению затрат является мозговой штурм. Он организуется и проводится руководителем единицы при поддержке членов рабочей группы. Участниками являются
сотрудники производственной единицы, а также представители смежников и заказчиков. В ходе мозгового штурма вырабатывается максимальное количество идей, направленных на сокращение затрат, повышение производительности и улучшение качества продукции. При этом
идеи не обсуждаются и не отбрасываются — фиксируются даже самые «сумасшедшие» идеи. Главной целью мозгового штурма является количество идей, а не их качество. Выработанные предложения оформляются в стандартном формате и заносятся в базу данных. После проведения
мозгового штурма идеи проходят предварительную оценку и сортируются по размеру финансового эффекта, риску внедрения, сроку окупаемости и простоте внедрения. Если количество и качество идей, выработанных в ходе мозгового штурма, недостаточно для сокращения
затрат на 40%, необходимо провести дополнительный опрос в цехах, привлечь экспертов и использовать опыт лучших компаний отрасли.

ЭТАП 4. ОЦЕНКА ПРЕДЛОЖЕНИЙ. На этом этапе оценивается сложность внедрения предложений, уточняется объем инвестиций и экономический эффект, определяются конкретные поставщики оборудования и услуг, предложения согласовываются со смежниками
и другими участниками. Входе анализа некоторые предложения отбрасываются и заменяются новыми. Таким образом, происходит постоянная итерация третьего и четвертого этапов. Результатом четвертого этапа является список реализуемых предложений, имеющих реальный
экономический эффект, со сроком окупаемости инвестиций, не превышающим двух лет. В конце четвертого этапа эти предложения выносятся на утверждение высшего руководства компании (Управляющего комитета).

ЭТАП 5. ПЛАНИРОВАНИЕ ВНЕДРЕНИЯ. Этап планирования начинается с утверждения идей на заседании Управляющего комитета. Руководитель единицы представляет идею членам комитета и объясняет, каким образом она может быть внедрена и как будет получен
экономический эффект. Презентация включает расчет финансового результата, требуемых инвестиций, сроков внедрения, определение ответственных, внешних поставщиков и партнеров. После утверждения предложения лидер единицы составляет подробный план внедрения, согласовывает
его с участвующими подразделениями и вносит соответствующие изменения в бюджет своей единицы.

ЭТАП 6. ВНЕДРЕНИЕ. Основной задачей этапа внедрения является контроль за достижением результатов, заявленных в утвержденных предложениях, осуществляемый специально созданной группой контроллинга. Она отслеживает фактическое расходование
средств в соответствии с утвержденными бюджетами, а также осуществляет непосредственный контроль над выполнением плана внедрения (своевременной установкой оборудования, проведением ремонтов и пр.). Группа контроллинга регулярно докладывает о ходе внедрения
Управляющему комитету.

Структура программы ТОП

Роли и задачи участников программы ТОП расписываются на каждом уровне организации. Высшее руководство компании, руководители и сотрудники производственных единиц несут основную ответственность за реализацию программы;специалисты оказывают методологическую
поддержку и обеспечивают организацию процесса.

Управляющий комитет руководит проектом, отвечает за внедрение программы, осуществляет контроль за результатами. Управляющий комитет проводит регулярные совещания для оценки, утверждения, а также контроля реализации предложений. В функции Управляющего комитета
также входит проверка предложений на соответствие общей стратегии развития компании.

Основная рабочая группа по выполнению программы ТОП состоит из специалистов (специально отобранных сотрудников предприятия, в основном из финансово–экономических и технологических служб, департамента бизнес–планирования). Она создается для поддержания руководителей
единиц в выработке и оценке предложений. Также ее задачей будет помощь в организации встреч и мозговых штурмов, структурирование анализа, сбор данных о показателях конкурентов, лучшем опыте в отрасли, доступных технологиях и др.

Руководители единиц совместно со своими сотрудниками отвечают за выработку и внедрение предложений по оптимизации производства. Руководители несут основную ответственность за достижение 40%–ного сокращения затрат.

«Железные правила» программы ТОП

Успех реализации программы зависит от строгого выполнения ряда основополагающих правил. Прежде всего, проект должен иметь безусловный приоритет в компании. Сроки, запланированные в программе, должны неукоснительно соблюдаться, совещания, в том числе с участием
высшего руководства, проводиться в назначенное время. Все подразделения должны быть поставлены в равные условия — цель сокращения затрат (на 40%) для всех одна и не меняется от специфики производственной единицы. Усилия всех участников процесса должны быть
направлены на достижение этой цели, руководители несут полную ответственность, исключающую оправдание за невыполнение поставленных задач.

Необходимо объявить «амнистию» за все прошлые ошибки, недоработки, упущенные возможности. Не прибавит стимула к плодотворной работе высказывания высших руководителей компании: «Ну что же вы раньше этого не сделали? Почему нужно было ждать, когда придут консультанты?».
Цель проекта — не разбираться с прошлыми ошибками и искать виновных, а направить внимание всех участников на будущее и открывающиеся возможности.

Не должно быть «священных коров» — все статьи затрат должны рассматриваться и ставиться под сомнение. Участники процесса должны быть мотивированы на то, чтобы идти на риск, предлагать неожиданные решения. Все возникающие вопросы по возможности должны решаться
на уровне руководителей единиц — передача ответственности «наверх» неприемлема.

Михаил Шамолин — консультант McKinsey, Москва

4.7. Оптимизация. Методы оптимизации

4.7.1. Общие сведения. Терминология

Некоторые
сведения об оптимизации, которые
необходимо учитывать при изучении
данного раздела, даны в § 1.13.

Проблема
оптимальности является одной из важнейших
в области конструирования и производства
ЭА, так как решение этой проблемы
позволяет повышать эффективность
изделий и технологических процессов.
Принятие тех или иных решений также не
обходится без применения методов
оптимизации.

Оптимизация
(от лат.
Optinum
– наилучшее) – это процесс нахождения
экстремума функции или выбор наилучшего
(оптимального) варианта из множества
возможных вариантов (альтернатив).

Какую
бы техническую задачу ни решал конструктор
или технолог, он всегда стремится
получить наилучший или оптимальный
ответ. Любая практически реализованная
конструкция или любой технологический
процесс могут рассматриваться с
определенной точки зрения как оптимальные,
так как имелись определенные основания
для предпочтения их остальным. Однако
в принципе выбор оптимального варианта
является сложной и трудоемкой задачей,
не решенной полностью до сих пор.

Если
рассматривать задачи оптимизации в
конструировании и технологии, то их
можно сформулировать следующим образом.

Задача
оптимизации в
конструировании
состоит в выборе наилучшего в некотором
определенном смысле варианта технического
решения из большого числа возможных
вариантов.

Задача
оптимизации в
технологии
состоит в том, чтобы наилучшим образом
построить технологический процесс и
определить оптимальные режимы его
проведения.

При разработке
конструкций ЭА и технологических
процессов ее производства решается
большое количество задач, из которых
вытекает многообразие задач оптимизации.

Так при конструировании
ЭА решаются задачи:

оптимизация
параметров;
оптимизация
структур по критериям минимальных
массы, затрат, габаритам, числу внутренних
и внешних связей, суммарной длине
соединительных проводников, числу
пересечений соединительных проводников,
магнитным и электрическим взаимодействиям;
оптимизация
конструкции модулей различных уровней
по надежности, тепловому режиму, по
размещению, по технологичности, по
стоимости;
оптимальное
резервирование с учетом ограничений
по массе, габаритам, стоимости;
оптимизация
требований к надежности элементов;
оптимизация
количества запасных элементов;
оптимизация
последовательности проверок ЭА при
ограниченном времени восстановления
и другие.

При
разработке производственных процессов
изготовления ЭА решаются задачи:

оптимизация
структуры производственного процесса
и его отдельных звеньев;
оптимизация
использования при производстве данного
изделия технологических процессов и
производств;
оптимизация
затрат труда, средств и времени на
изготовление изделия;
оптимизация
номенклатуры технологических документов,
применяемых в качестве директивных;
оптимизация
типовых, групповых и пр. технологических
процессов;
оптимизация
раскроя материалов и другие.

Прежде
чем приступить к изучению математических
методов оптимизации, необходимо
ознакомиться с рядом понятий.

Объект
оптимизации
– система или изделие, подвергаемые
оптимизации.

Факторное
пространство
– это пространство (область) Х
с координатами
,
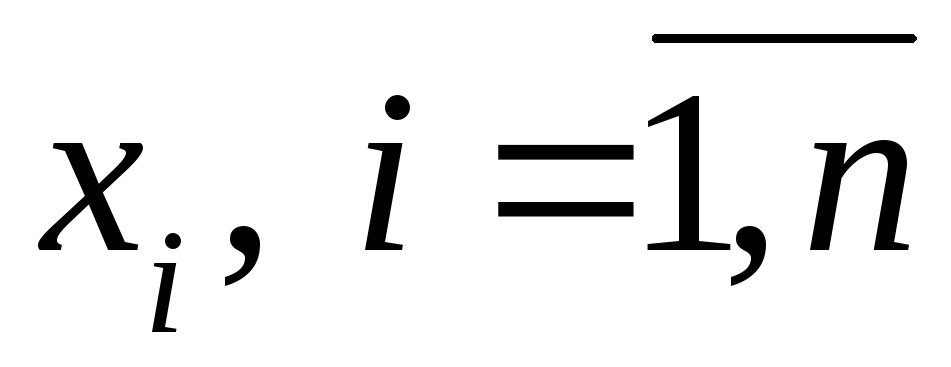которые соответствуют независимым
переменным системы, варьируемым при
исследовании.

Функция
отклика
F
(целевая функция) – функция, связывающая
параметр оптимизации y
с переменными, варьируемыми при
исследовании

y
= F(x₁,
x₂,
…, x_n).

Поверхность
отклика
– геометрическое изображение функции
отклика в факторном пространстве.

При
изложении вопросов, связанных с поиском
экстремума, полезно использовать
графическое изображение поверхности
отклика и траектории движения от исходной
точки к экстремальной в пространстве
управляемых параметров, получающейся
в результате ряда последовательных
шагов поиска.

Поверхность
отклика функции изображают в виде
совокупности линий равного уровня.
Линия равного уровня – множество точек
пространства, в которых рассматриваемая
функция имеет одинаковые значения,
равные заданной величине (при двух
переменных x₁
и x₂).
При трех переменных линии равного уровня
становятся поверхностными, а при п
> 3 – гиперповерхностными равного
уровня (рис. 4.14)

Изображающая
точка –
точка в факторном пространстве,
характеризующая состояние системы (в
рассматриваемый момент времени).

Глобальный
экстремум
– это наибольшее (наименьшее) значение
функции отклика F(x₁,…,
x_n)
в пределах всей области Х
переменных x_i
(точка 0₁
на рис. 4.14).

Локальный
экстремум
– это наибольшее (наименьшее) значение
функции отклика F(x₁,
…, x_n)
в некоторой точке
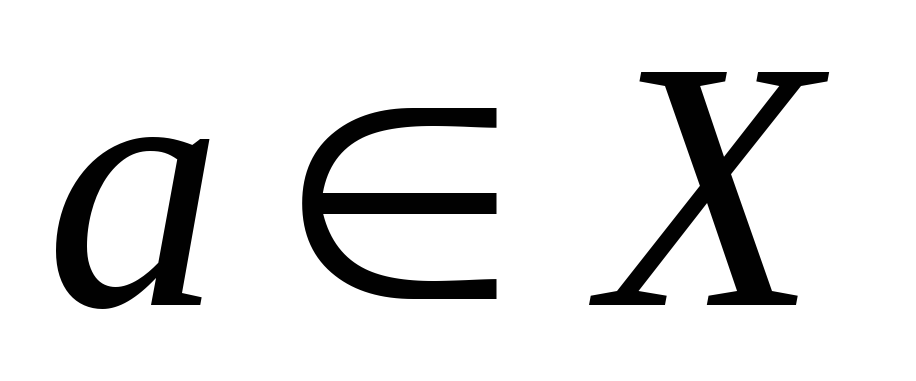по сравнению с ее значениями в точках,
принадлежащих малой окрестности точки(точка 0₂
на рис. 4.14).

Если
в пределах области Х
имеется всего один экстремум, то он
обязательно будет глобальным.

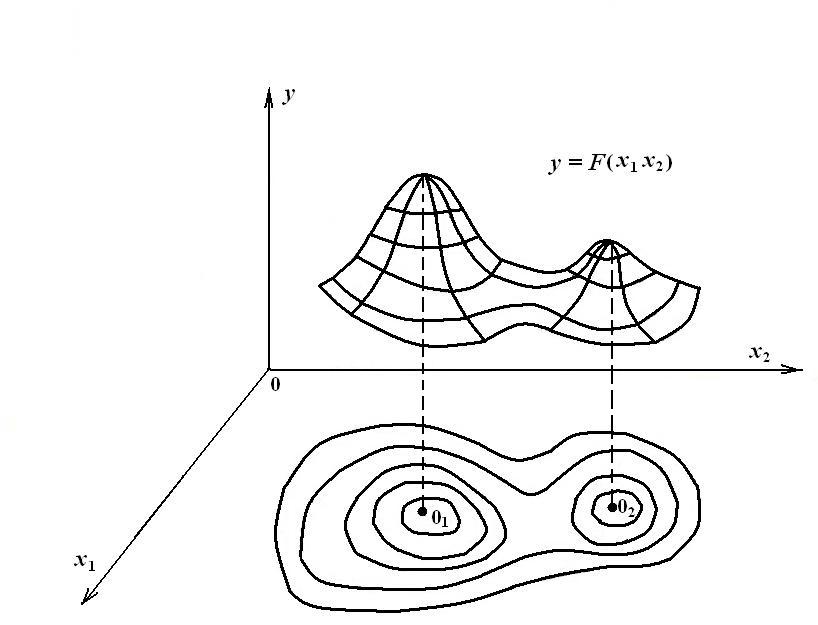
Рисунок 4.14.

Экстремум
называется граничным,
если он имеет место в граничных точках
области Х,
и внутренним,
если он соответствует внутренней точке
области Х.

Экстремум
называется безусловным,
если на переменные x_i
не накладывается никаких ограничений,
и условным,
если переменные x_i
связаны ограничениями типа равенств.

При оптимизации
могут решаться задачи:

– задача классической
оптимизации;

– задача
неклассической оптимизации.

Классическая
задача оптимизации заключается в
оптимизации целевой функции

y
= F(x₁,
x₂,
…, x_n)
= extr,

т.е.
определяются такие значения независимых
переменных (проектных параметров) x_i,
при которых целевая функция приобретает
экстремальное значение с учетом всякого
рода ограничений.

Неклассическая
задача оптимизации имеет место, когда
неизвестна функциональная зависимость
между показателем качества (параметром
оптимизации) y
и параметрами x_i.
Поэтому в такой задаче оптимизируется
не только целевая функция, но и сам
способ оптимизации. Другими словами
при неклассической задаче оптимизации
выбирают также оптимальную стратегию
поиска экстремума, а не только оптимальное
значение параметра оптимизации y.

В
общей структуре проектирования и
изготовления электронной аппаратуры
можно выделить три этапа оптимизации:

– структурная
оптимизация
– выбор наилучшей конструкторской
реализации ЭА, обеспечивающей выполнение
заданных функциональных требований;

– параметрическая
оптимизация
– выбор наилучшего соотношения
номинальных параметров, обеспечивающих
заданные электрические характеристики,
и определение допусков на параметры
элементов по допустимому отклонению
выходных параметров;

– технологическая
оптимизация
– выбор номинальных значений
конструкционных параметров и
технологической точности на них, исходя
из производственных и экономических
требований.

На
каждом из этапов встает проблема
формулировки критерия оптимальности
и оптимального решения задачи. Однако
системный подход подразумевает общую
оптимизацию проектирования и изготовления
ЭА, так что в отдельности каждое из них
может и не быть оптимальным.

Общая
форма показателя оптимальности
(эффективности функционирования) должна
вытекать из основного постулата
исследования операций: оптимальным
решением
является то решение, которое обеспечивает
выполнение поставленной задачи при
минимуме материальных затрат, либо то,
которое обеспечивает выполнение
поставленной задачи с максимальной
эффективностью при фиксированных
материальных затратах [44*].

Обзор основных методов математической оптимизации для задач с ограничениями / Habr

Я долго готовился и собирал материал, надеюсь в этот раз получилось лучше. Эту статью посвящаю основным методам решения задач математической оптимизации с ограничениями, так что если вы слышали, что симплекс-метод — это какой-то очень важный метод, но до сих пор не знаете, что он делает, то возможно эта статья вам поможет.

P. S. Статья содержит математические формулы, добавленные макросами хабраредактора. Говорят, что они иногда не отображаются. Также есть много анимаций в формате gif.

Преамбула

Задача математической оптимизации — это задача вида «Найти в множестве элемент такой, что для всех из выполняется », что в научной литературе скорее будет записано как-то так

Исторически так сложилось, что популярные методы такие как градиентный спуск или метод Ньютона работают только в линейных пространствах (причем желательно простых, например ). На практике же часто встречаются задачи, где нужно найти минимум не в линейном пространстве. Например нужно найти минимум некоторой функции на таких векторах , для которых , это может быть обусловлено тем, что обозначают длины каких-либо объектов. Или же например, если представляют координаты точки, которая должна быть на расстоянии не больше от , т. е. . Для таких задач градиентный спуск или метод Ньютона уже напрямую не применить. Оказалось, что очень большой класс задач оптимизации удобно покрывается «ограничениям», подобными тем, что я описал выше. Иначе говоря, удобно представлять множество в виде системы равенств и неравенств

Задачи минимизации над пространством вида таким образом стали условно называть «задачами без ограничений» (unconstrained problem), а задачи над множествами, заданными наборами равенств и неравенств — «задачами с ограничениями» (constrained problem).

Технически, совершенно любое множество можно представить в виде одного равенства или неравенство с помощью индикатор-функции, которая определяется как

однако такая функция не обладает разными полезными свойствами (выпуклость, дифференцируемость и т. п.). Тем не менее, часто можно представить в виде нескольких равенств и неравенств, каждое из которых такими свойствами обладает. Основная теория подведена под случай

где — выпуклые (но не обязательно дифференцируемые) функции, — матрица. Для демонстрации работы методов я буду использовать два примера:

Задача линейного программирования
$$display$$\begin{array}{rl} \mbox{минимизировать } & -2&x~~~- &y \\ \mbox{при условии } &-1.0 & ~x -0.1 & ~y \leq -1.0 \\ & -1.0 & ~x + ~0.6 &~ y \leq -1.0 \\ & -0.2 & ~x + ~1.5 & ~y \leq -0.2\\ & ~0.7 &~x + ~0.7 & ~y \leq 0.7\\ &~2.0 & ~x -0.2 & ~y \leq 2.0\\ &~0.5 & ~x -1.0 & ~y \leq 0.5\\ &-1.0 & ~x -1.5& ~ y \leq -1.0\\ \end{array} $$display$$

По сути эта задача состоит в том, чтобы найти самую дальнюю точку многоугольника в направлении (2, 1), решение задачи — точка (4.7, 3.5) — самая «правая» в многоугольнике). А вот собственно и сам многоугольник

Минимизация квадратичной функции с одним квадратичным ограничением

Симплекс-метод

Из всех методов, которые я покрываю этим обзором, симплекс-метод наверно является самым известным. Метод был разработан специально для линейного программирования и единственный из представленных достигает точного решения за конечное число шагов (при условии, что для вычислений используется точная арифметика, на практике это обычно не так, но в теории возможно). Идея симплекс-метода состоит из двух частей:

Системы линейных неравенств и равенств задают многомерные выпуклые многогранники (политопы). В одномерном случае это точка, луч или отрезок, в двумерном — выпуклый многоугольник, в трехмерном — выпуклый многогранник. Минимизация линейной функции — это по сути нахождение самой «дальней» точки в определенном направлении. Думаю, интуиция должна подсказывать, что этой самой дальней точкой должна быть некая вершина, и это действительно так. В общем случае, для системы из неравенств в -мерном пространстве вершина — это точка, удовлетворяющая системе, для которой ровно из этих неравенств обращаются в равенства (при условии, что среди неравенств нет эквивалентных). Таких точек всегда конечное число, хоть их и может быть очень много.

Теперь у нас есть конечный набор точек, вообще говоря можно их просто взять и перебрать, то есть сделать что-то такое: для каждого подмножества из неравенств решить систему линейных уравнений, составленных на выбранных неравенствах, проверить, что решение подходит в исходную систему неравенств и сравнить с другими такими точками. Это довольно простой неэффективный, но рабочий метод. Симплекс-метод вместо перебора двигается от вершины к вершине по ребрам таким образом, чтобы значений целевой функции улучшалось. Оказывается, если у вершины нет «соседей», в которых значений функции лучше, то она оптимальна.

Симплекс-метод является итеративным, то есть он последовательно по чуть-чуть улучшает решение. Для таких методов нужно с чего-то начинать, в общем случае это делается с помощью решения вспомогательной задачи

Если для решения этой задачи такое, что , то выполняется , иначе исходная задача вообще задана на пустом множестве. Чтобы решить вспомогательную задачу, можно также использовать симплекс-метод, начальной же точкой можно взять с произвольным . Нахождение начальной точки можно условно назвать первой фазой метода, нахождение решение исходной задачи можно условно назвать второй фазой метода.Траектория двухфазового симплекс-методаТраектория была сгенерирована с помощью scipy.optimize.linprog.

Проективный градиентный спуск

Про градиентный спуск я недавно писал отдельную статью, в которой в том числе кратко описал и этот метод. Сейчас этот метод вполне себе живой, но изучается как часть более общего проксимального градиентного спуска. Сама идея метода совсем банальна: если мы применяем градиентный спуск к выпуклой функции , то при правильном выборе параметров получаем глобальный минимум . Если же после каждого шага градиентного спуска корректировать полученную точку, взяв вместо нее её проекцию на замкнутое выпуклое множество , то в результате мы получим минимум функции на . Ну или более формально, проективный градиентный спуск — это алгоритм, который последовательно вычисляет

где

Последнее равенство определяет стандартный оператор проекции на множество, по сути это функция, которая по точке вычисляет ближайшую к ней точку множества . Роль расстояния здесь играет , стоит отметить, что здесь можно использовать любую норму, тем не менее проекции с разными нормами могут отличаться!

На практике проективный градиентный спуск используется только в особых случаях. Основная его проблема состоит в том, что вычисление проекции может быть еще более сложной задачей, чем исходная, а её нужно вычислять много раз. Самый распространенный случай, для которого удобно применять проективный градиентный спуск — это «коробочные ограничения», которые имеют вид

В этом случае проекция вычисляется очень просто, по каждой координате получается

Применение проективного градиентного спуска для задач линейного программирования совершенно бессмысленно, тем не менее если это все-таки сделать, то выглядеть будет как-то такТраектория проективного градиентного спуска для задачи линейного программирования

А вот как выглядит траектория проективного градиентного спуска для второй задачи, есливыбирать большой размер шага

и если выбирать небольшой размер шага

Метод эллипсоидов

Этот метод примечателен тем, что является первым полиномиальным алгоритмом для задач линейного программирования, его можно считать многомерным обобщением метода бисекции. Я начну с более общего метода разделяющей гиперплоскости:

На каждом шаге метода есть некоторое множество, которое содержит решение задачи.

На каждом шаге строится гиперплоскость, после чего из множества удаляются все точки, лежащие по одну сторону выбранной гиперплоскости, и, возможно, к этому множеству добавятся какие-то новые точки

Для задач оптимизации построение «разделяющей гиперплоскости» основано на следующем неравенстве для выпуклых функций

Если зафиксировать , то для выпуклой функции полупространство содержит только точки со значением не меньше, чем в точке , а значит их можно отсечь, так как эти точки не лучше, чем та, что мы уже нашли. Для задач с ограничениями можно аналогичным образом избавиться от точек, которые гарантированно нарушают какое-то из ограничений.

Самый простой вариант метода разделяющей гиперплоскости — это просто отсекать полупространства без добавления каких-либо точек. В результате на каждом шаге у нас будет некий многогранник. Проблема этого метода в том, что количество граней многогранника скорее всего будет возрастать от шага к шагу. Более того, оно может расти экспоненциально.

Метод эллипсоидов собственно на каждом шаге хранит эллипсоид. Точнее, после проведения гиперплоскости строится эллипсоид минимального объема, который содержит одну из частей исходного. Этого получается добиться за счет добавления новых точек. Эллипсоид всегда можно задать положительно определенной матрицей и вектором (центром эллипсоида) следующим образом

Построение минимального по объему эллипсоида, содержащего пересечение полупространства и другого эллипсоида, можно осуществить с помощью в меру громоздких формул. К сожалению на практике этот метод оказался все еще на так хорош, как симплекс-метод или метод внутренней точки.

А вот собственно как он работает для

линейного программирования

и дляквадратичного программирования

Метод внутренней точки

Этот метод имеет долгую историю развития, одни из первых предпосылок появились примерно в то же время, когда был разработан симплекс-метод. Но в то время он был еще недостаточно эффективен, чтобы использоваться на практике. Позднее в 1984 был разработан вариант метода специально для линейного программирования, который был хорош как в теории, так и на практике. Более того, метод внутренней точки не ограничен только линейным программированием в отличие от симплекс-метода, и сейчас он является основным алгоритмом для задач выпуклой оптимизации с ограничениями.

Базовая идея метода — замена ограничений на штраф в виде так называемой барьерной функции. Функция называется барьерной функцией для множества , если

Здесь — внутренность , — граница . Вместо исходной задачи предлагается решать задачу

и заданы только на внутренности (по сути отсюда и название), свойство барьера гарантирует, что у минимум по существует. Более того, чем больше , тем больше влияние . При достаточно разумных условиях можно добиться того, что если устремить к бесконечности, то минимум будет сходиться к решению исходной задачи.

Если множество задано в виде набора неравенств , то стандартным выбором барьерной функции является логарифмический барьер

Точки минимума функции для разных образует кривую, которую обычно называют центральный путь, метод внутренний точки как бы пытается следовать этому пути. Вот так он выглядит для Примера с линейным программированием
Аналитический центр — это просто

Наконец сам метод внутренней точки имеет следующий вид

Выбрать начальное приближение ,

Выбрать новое приближение методом Ньютона

Увеличить

Использование метода Ньютона здесь очень важно: дело в том, что при правильном выборе барьерной функции шаг метода Ньютона генерирует точку, ~~которая остается внутри нашего множества~~, поэкспериментировали, в таком виде не всегда выдает. Ну и наконец, так выглядит траектория метода внутренней точкиЗадача линейного программирования
Прыгающая черная точка — это , т.е. точка, к которой мы пытаемся приблизиться шагом метода Ньютона на текущем шаге.

Задача квадратичного программирования

Оптимизация производственных процессов и объема производства

Если верить Минэкономразвития РФ, то оптимизация производственных процессов,
весьма вяло проводившаяся в стране (а иногда и вовсе не наблюдавшаяся!), не
позволила России войти в число государств, способных продемонстрировать высокие
темпы промышленного развития. Естественно, нефтегазовое направление брать в
расчет нельзя, там многое зависит от конъюнктуры рынка. Красноречивые и вполне
официальные цифры: отставание в производительности труда российского
промышленного комплекса в 2010 году по сравнению со странами Евросоюза и США
составляло 30 раз. Отрадно, что этот дисбаланс планируется нивелировать
примерно до 2,5 раза к 2020 году, однако история подобного еще не знала. И все
же можно утверждать, что адаптированный к нашим реалиям опыт наиболее развитых
экономик мира является существенным подспорьем, способным оказать положительное
влияние на такое явление, как оптимизация
объема производства в России.

Читайте также: Автоматизация производственных процессов..

Семантическое
уточнение.
Зачастую значение слова «оптимизация»
воспринимается как «улучшение», «совершенствование». Особенно это характерно
для нетехнического языка. В действительности термин обозначает нахождение
наилучшего решения в какой-либо области. Сейчас на постсоветском пространстве
под «оптимизацией» почему-то понимается снижение, сокращение количества. И под
этим лозунгом увольняют рабочих, госслужащих, уменьшают количество койко-мест в
больницах и т. д. Во-вторых, выработать самый эффективный способ управления
предприятием – не значит взять какую-то одну модель и настойчиво пытаться ее
реализовать на практике. Методология предполагает поливариативность концепций,
их сортировку с помощью «мозгового штурма» и определение самой приемлемой.

Производственные линии

Концепции оптимизации процесса производства

Оптимизация
процесса производства в современном формате предлагает
российским компаниям несколько вариантов совершенствования, построенных на
разных принципах. Выбор между ними зависит от результатов анализа, который
рекомендуется проводить с привлечением сторонних организаций. Первый, «тотальная оптимизация производства продукции»,
базируется на максимальном участии всего коллектива в деле повышения
эффективности. Создаются рабочие группы, рассматривающие рационализаторские
решения, определяются программы снижения затрат, инвестиционные проекты и т.д.
Фактически, успех всех усилий зависит от того, сумеет ли руководство субъекта
хозяйствования добиться раскрытия творческого потенциала коллектива завода,
организации, фирмы и др.

Второй метод – «бережливое предприятие» –
предполагает оценку того, какие качественные характеристики продукции важнее
всего клиенту. Когда они выявлены, из технологической цепочки исключают не
создающие конечной ценности товара процессы – транспортировку лишних материалов,
их промежуточное хранение на складах, ненужное перемещение персонала и т. д. Оптимизация производственных процессов
в таком случае всегда связана с тем, что какой-либо участок или цех не
запускает оборудование до тех пор, пока следующее в технологической цепочке
подразделение не подаст заявку о потребности в деталях/комплектующих.

Разумеется, станочное оборудование переходит на
производство небольших партий изделий. Казалось бы, парадокс: если завод
ориентирован на массовый выпуск, производственные простои только увеличат
себестоимость продукции. И все-таки многочисленные примеры западных компаний
доказывают реалистичность такого реформирования. Но проводить его следует при
возможности быстрой смены оборудования в сжатые сроки. То есть оптимизация объема производства в
концепции «бережливое предприятие» требует гибкости как конвейерных линий, так
и всех единиц оборудования.

Принципиальный вопрос №2 – это грамотная организация
рабочих мест, при которой инструменты и детали располагаются максимально
удобным образом. В данном разрезе актуально использование эргономичной промышленной мебели: монтажно-сборочных столов, подкатных тележек и т. д.
Таким образом достигается увеличение
производительности производства промышленного персонала до 40%.

Оптимизация технологических процессов: методы, основы и задачи

Основные задачи

Оптимизация технологических процессов помогает сделать наиболее эффективный выбор рационального варианта в конкретной ситуации. Главными задачами расчетов при этом выступают следующие:

Выбор оптимального критерия. Это могут быть различные параметры, чаще всего, минимальная себестоимость при наибольшей производительности, максимальной нагрузке на технологическое оборудование. В некоторых случаях эффективнее будет использовать не один параметр, а несколько, добиваясь самого результативного решения.
Определение параметра, который будет оказывать влияние на результативность ТП.
Разработка F = F(X) в зависимости от существующих условий модели (например, если определяющим параметром стала наименьшая себестоимость, то в данном случае целевой будет зависимость от имеющихся параметров).
Выполняется поиск оптимального решения с вычислением экстремума, нахождением наиболее подходящего для конкретной ситуации технологического процесса.

Виды оптимизации

Виды основ оптимизации ТП (технологических процессов) включают в себя параметрические и структурные рабочие методы. Первая группа – это изменение имеющихся значений при определенной структуре, например, расчет оптимального состава режима использования оборудования или реза. Чтобы решить такие задачи, необходимо использование нелинейного либо линейного математического программирования.

Структурная оптимизация процесса проектирования связана с подбором структуры, она работает по принципу исключения вариантов за счет следующего:

вмешательство в уже осуществляемое проектирование с целью поиска самого лучшего и результативного решения с определенной точки зрения и в соответствии с заданными значениями;
унификация выбранных вариантов.

Методы

Оптимизация параметров для технологического процесса решает задачу выбора метода, при котором наименьшие затраты на вычисление дадут больший информационный объемом о требуемом процессе.

Процессы находятся в прямой зависимости от того, какие именно методы будут применены в работе при поиске наиболее результативного решения для конкретной ситуации. Всего можно выделить пять методов, включающих в себя:

аналитические, в ходе применения которых осуществляется поиск лучшего варианта среди имеющихся;
программирование, эта группа включает в себя линейные, динамические, геометрические методы, учитывающие оптимизацию, выбор наиболее результативного процесса;
градиентные с ограничением или без ограничения;
автоматические самонастраиваемые, которые будут оптимальными для очень сложных систем;
статические или активные, использующие различные подходы (активный поиск или пассивное наблюдение).

Оптимизация для технических процессов применяется для выбора оптимального варианта из имеющихся, то есть фактически это выполняемый поиск экстремума для F(X) при помощи варьирования имеющихся проектных (заданных предварительно) значений для X в пределах следующей области допущения: extr F(X), X € D_x, при этом используются следующие параметры:

F(X) – используемая функция;
X – вектор переменных;
D_x – допустимая рабочая область X.

Выбор будет индивидуальным, он соответствует заданным процессам и условиям. Чаще всего это наименьшая себестоимость, то есть самые меньшие финансовые затраты, максимально возможная производительность при заданных условиях с наименьшим временем, необходимым для изготовления одной единицы.

Методы оптимизации технологических процессов могут использовать один или несколько критериев, то есть в работе будут применяться различные параметры, многокритериальная оптимизация. При этом будет создан один компромиссный критерий, учитывающий сразу несколько выбранных параметров, так называемых Еi-локальных критериев (Е₁, Е₂, Е₃, …Е_r). Для каждого такого критерия будет решаться задача оптимизации разработки технологических процессов, после чего будет выполнено вычисление экстремального значения для Е_i (при i, равном 1, 2, 3, …, r).

Уравнение отклонения для критерия будет записано таким образом: Q_i = E_i - E_i*. Отдельно для каждого из них следует вычислить весовой коэффициент λ_i (0 i ∑ λ_i = 1), что необходимо для определения важности параметра в рамках технологического процесса. Для записи компромиссного критерия применяется аддитивная функция Q = ∑ Q_i λ_i. Только после этого решается оптимизация параметров процесса. Для решения могут применяться различные методы, включая имитационные, аналитические, комбинированные.

Аналитические методы оптимизации технологического процесса производства предполагают применение средств математического программирования. Всего четырнадцать таких методов, включая покоординационный подъем, градиентный, исключения областей, дихотомии, деления интервала, Фиббоначи, Розенбока и другие.

Имитационная оптимизация управления технологическими процессами предполагает работу в реальных условиях, создания имитационной модели, основа которой дает возможность выбрать удовлетворяющий вариант ТП. При расчетах применяются способы исключения, выбора подходящей модели, что позволяет достигнуть заданного критерия. При моделировании применяются такие языки, как GPSS, Симула, Симскрипт.

Комбинированный метод предполагает использование отдельных приемов указанных приемов, объединение аналитического и имитационного методов в один, что позволяет достигнуть оптимального результата. Такой способ применяется при определенных условиях и необходимости получения наиболее точного результата.

Выбор метода полностью зависит от ситуации, условий расчетов и прочих данных, включая требования к результативности. Часто оптимальным является комбинированный метод, более гибкий и позволяющий работать практически при любых ситуациях. Советуем вам также почитать про методы структурирования информации.

Задачи оптимизации производства — Энциклопедия по экономике

Нелинейное программирование. Оно объединяет методы решения задач, которые описываются нелинейными соотношениями. Постановка и решение задач нелинейного программирования принципиально не отличаются от постановки и решения задач линейного программирования. К задачам нелинейного программирования относятся задачи оптимизации производства для большинства предприятий, поскольку в настоящее время они действуют на неоднородном рынке в условиях монополистической конкуренции и спрос на их продукцию зависит от цены. [c.114]

В других главах непосредственно излагаются отдельные разделы микроэкономики, но акцент при этом делается на математическом обосновании соответствующих утверждений. При этом предполагается, что связанные с этим вопросы содержательного характера обсуждаются в основном в курсе микроэкономики, полностью скоординированном и читаемом параллельно с курсом математических методов. Здесь имеются в виду главы и разделы по теории потребительского выбора, производственным функциям, задачам оптимизации производства, моделированию экономической динамики, статистическому оцениванию макроэкономических зависимостей. [c.10]

ЗАДАЧИ ОПТИМИЗАЦИИ ПРОИЗВОДСТВА [c.178]

Глава II. Задачи оптимизации производства 179 [c.179]

Глава П. Задачи оптимизации производства 181 [c.181]

Задача оптимизации производства для предприятия ставится в форме максимизации выручки или прибыли при заданных ассортименте выпускаемой продукции и ограничениях на имеющиеся запасы ресурсов (сырье, оборудование, труд, производственные площади и др.). Задача может ставиться и в форме минимизации затрат при выпуске заданных объемов продукции несколькими способами производства. Оптимизационные задачи могут быть поставлены не только для предприятий реального сектора экономики, но также и для торговли, банковской и страховой деятельности. [c.44]

Все это способствует повышению уровня аналитической № нормативной работы, большей обоснованности решений. Внедрение АСУП позволяет определять ряд аналитических показателей, расчет которых затруднен фондо-, материале- и трудоемкость. Использование их для планирования и анализа позволяет более четко устанавливать затраты на производство каждого продукта и пути их снижения, определять влияние структурных изменений (изменение ассортимента продукции) на конечные показатели работы предприятия. При расчете экономической эффективности АСУП учитывают экономический эффект, достигаемый в результате оптимизации производства и снижения трудоемкости решения учетных задач. [c.305]

Задача оптимизации формулируется следующим образом необходимо находить и постоянно поддерживать такие управляющие воздействия, которые обеспечат достижение максимального (или минимального) значения целевой функции, зависящей от вектора управляющих и возмущающих воздействий (контролируемых и неконтролируемых). Целевой функцией при осуществлении процесса может быть один из следующих технико-экономических показателей прибыль, количество выпускаемой товарной продукции, затраты на производство и т. д. Наиболее общим из перечисленных критериев является прибыль П, которая для производства полипропилена в укрупненном виде выражается следующим образом [c.423]

Новые возможности для использования всех рассмотренных выше методов открываются применением в планировании методов экономико-математического моделирования. Так, например, аппарат межотраслевого моделирования позволяет увязать баланс народного хозяйства с системой материальных балансов, с отраслевыми расчетами потребности в продукции и структуры затрат на ее производство, с расчетами по капитальному строительству, уровню жизни населения и др., а в конечном счете — поставить и решить задачу оптимизации межотраслевых связей. Тем самым балансовый метод получает свое дальнейшее развитие за счет применения методов межотраслевого моделирования и оптимального планирования. Методы сетевого планирования, матричной алгебры, оптимизации выступают в качестве инструментов практической реализации программно-целевого подхода, а методы математической статистики находят широкое применение в прогнозировании. [c.95]

БП—блоки оптимизационных задач. В таких блоках могут объединяться двух-трехуровневые системы оптимизации расчетов. Примером такого блока может служить блок оптимизации агропромышленного комплекса, включающий однопродуктовые задачи оптимизации развития и размещения производства (например, по отдельным сельскохозяйственным культурам), многопродуктовые задачи того же типа (например, по растениеводству в целом) и задачу оптимизации по всему агропромышленному комплексу [c.136]

Следует отметить, что методы оптимизации находят применение и в задачах текущего планирования. Так, ГВЦ Госплана СССР совместно с отделом легкой промышленности Госплана СССР в течение уже ряда лет решаются задачи оптимизации годовых планов производства тканей, тюлегардинных изделий, обуви. В этих задачах определяется такой вариант объема и структуры производства продукции данной подотрасли, который обеспечивает наиболее полное удовлетворение потребностей народного хозяйства и населения при заданных ограничениях по материальным ресурсам (прежде всего — исходному сырью) и производственным мощностям с учетом планируемого уровня их использования. [c.213]

Организационная структура российских предприятий -наследство плановой экономики. В условиях, когда финансовые и материальные ресурсы жестко лимитировались государством для достижения определенных производственных результатов, такое разбиение производства по функциональным звеньям полностью оправдывало себя. Рыночная экономика диктует свои правила игры компании вынуждены сами формировать стратегию, изыскивать ресурсы для обеспечения своей деятельности и эффективно их использовать с целью достижения определенного финансового результата. Однако существующая организационная система, как совокупность функциональных звеньев, не позволяет решить задачу оптимизации финансовых и материальных потоков и, самое главное, не позволяет контролировать расходование этих ресурсов в процессе производства. Для устранения диссонанса между целью системы и ее [c.92]

В современных рыночных условиях развития нефтеперерабатывающих и нефтехимических предприятий в России, обострения конкуренции между отдельными заводами и нефтяными компаниями все более важными становятся вопросы повышения эффективности функционирования производства. И в первую очередь разрешение этих вопросов связано с улучшением методологии и инструментария производственного и инвестиционного планирования, решением задач оптимизации (с точки зрения максимизации получаемой прибыли или минимизации производственных затрат) производственных планов, отражающих различные сценарии изменения рыночного окружения и технологического состояния производства. [c.331]

Задачи оптимизации современным производством обычно являются многоцелевыми (многокритериальными). К основным критериям управления можно отнести повышение производи- [c.16]

Повышение эффективности основного производства ГДП достигается за счет автоматизированных расчетов на ЭВМ технологических режимов работы оборудования и выбора наиболее рациональных режимов эксплуатации, промысловых объектов. Использование ЭВМ для регулирования технологических процессов позволяет уточнить расчеты сменного диспетчера и значительно увеличить их объем, что является промежуточным этапом внедрения оптимальных систем управления и служит предпосылкой успешного освоения сменным диспетчером необходимых навыков работы при переходе к решению задач оптимизации [38]. [c.99]

Регулирование технологических процессов добычи и подготовки газа предусматривает стабилизацию параметров процессов, для чего используются системы автоматического регулирования давлений, температур, соотношений технологических потоков, качественных показателей газа и конденсата. Задания для регулирования выбираются на основе решения задач расчета технологических режимов. Этот комплекс задач состоит из локальных задач рационального распределения нагрузки и расчета рациональных режимов работы технологического оборудования, решаемых на конкретных технологических установках, обеспечивающих добычу и подготовку газа и конденсата к транспорту. Решение задач оперативного регулирования режимов работы объектов основного производства дает информационную основу для последующего решения задач оптимизации режимов работы объектов добычи и подготовки газа к транспорту, заключающейся в выборе и поддержании наивыгоднейших технологических [c.99]

Оптимальным считается такой объем реализации, который обеспечивает получение максимальной прибыли при сложившихся условиях производства в определенном ценовом диапазоне. Задача оптимизации больше теоретическая, чем практическая, однако оптимальный объем при планировании выпуска продукции является тем ориентиром, знание которого необходимо. [c.131]

В этой главе мы рассмотрели приемы линейного программирования при решении задач оптимизации. Типичный пример — максимизация прибыли предприятия за счет определения соответствующей номенклатуры производства. Кроме того, задачи линейного программирования могут быть направлены на минимизацию переменных, в частности затрат. Выражение, которое необходимо оптимизировать, называется объективной функцией. Эта функция высчитывается при наличии ряда ограничений. Одна из самых больших трудностей при решении такого рода задач состоит в исходной постановке задачи, когда необходимо определить ограничения, представить их в виде неравенств и выдать выражение объективной функции. При решении простых задач только с двумя переменными можно применить графический метод. Для более сложных задач применяется симплексный метод. [c.304]

Линейное и целочисленное программирование используется для принятия управленческих решений в таких областях, как планирование и составление графиков производства, создание и расходование складских запасов, финансовое планирование, отбор портфеля заказов, маркетинг и реклама товаров компаний и т. п. Тем не менее при всей своей прогностической способности линейное и целочисленное программирование не отличается высокой степенью предвидения элементов неоднозначности. Уже давно концептуально решена задача оптимизации поставленной цели, зависящей от ряда ограничительных факторов. Интуиция и здравый смысл являются серьезными помощниками при решении довольно простых задач и позволяют оптимизировать результат решения задачи без специальных знаний и сложных методик количественной оценки. Однако при решении сложных задач, включающих сотни переменных и ограничителей, интуиция и здравый смысл помогают мало. [c.254]

Во-первых, базовая модель анализа, изображенная на рис. 1, решает задачу нахождения оптимальной величины физического объема сбыта и уровня цен реализации для одного вида продукции. При ограниченных ресурсах предприятия и наличии широкого ассортимента сбыта на практике часто необходимо решать задачи оптимизации структуры производства и сбыта, исходя из сравнения планируемого дохода от реализации различных видов продукции. Это в достаточной степени усложняет алгоритм СКР-анализа. [c.45]

Цель классификации задач оптимизации — показать, что эти задачи, различные по своему содержанию, можно решать на компьютере с помощью стандартных программных продуктов. Классификацию задач оптимизации, возникающих на производстве, можно выполнить по следующим признакам область применения содержание задачи класс экономико-математических моделей. [c.103]

Раздельное решение задач не обеспечивает нахождения оптимальных плановых решений, и это нашло отражение в структуре системы моделей оптимального текущего планирования нефтеперерабатывающего производства [1], включающей отраслевую модель оптимизации производства и распределения нефтепродуктов, модель линейного программирования комплекса НПП и модель линейного программирования НПП, обеспечивающих расчет производственной программы отдельных предприятий, распределение плановых заданий между комплексами предприятий. [c.12]

Учитывая указанные обстоятельства, представляется целесообразным использование многоэтапной постановки стохастической задачи оптимизации календарного планирования основного производства НПП с жесткими условными вероятностными ограничениями следующего вида [c.60]

На нефтеперерабатывающих производствах значимая корреляция между технологическими коэффициентами а,-у и компонентами Ь/ вектора ограничений, которую следовало бы учитывать при формализации задачи оптимизации, также не наблюдается. Это связано с тем, что в соответствии с существующей схемой переработки нефти и нефтепродуктов целевая продукция НПП вырабатывается в товарном блоке в результате реализации специальной операции компаундирования. Кроме того, на [c.69]

ЗАДАЧА ОПТИМИЗАЦИИ КАЛЕНДАРНЫХ ПЛАНОВ НЕФТЕПЕРЕРАБАТЫВАЮЩИХ ПРОИЗВОДСТВ [c.75]

Эти обстоятельства обусловливают необходимость разработки вероятностных динамических постановок и соответствующих стохастических моделей задач оптимизации календарных планов нефтеперерабатывающих производств. [c.78]

Разбивка годовой производственной программы на календарные отрезки времени осуществляется на основе вероятностной модели многоэтапной стохастической задачи оптимизации календарною планирования основного производства НПП. [c.177]

В многономенклатурном химическом производстве, где им. ется возможность варьировать номенклатуру и ассортимент выпускаемой продукции, возникает задача оптимизации производственной программы, т. е. выбора оптимального ассортимента продукции. [c.190]

Рассматриваемый подход анализа изделия как системы, состоящей из нескольких узлов, способствует решению еще одной важной задачи — оптимизации надежности и себестоимости электроизделий (электрических машин, аппаратов и др.) при их функционировании в системах автоматизации. Каждый отказ электроизделий приводит во многих случаях к отказу всей системы автоматизированного электропривода. Поэтому относительно высокие показатели надежности электроизделий в ряде случаев оказываются недостаточными с точки зрения требований АСУТП. Задача оптимизации надежности и себестоимости электроизделий с точки зрения их работы в системах решается на основе принципов, изложенных выше. При этом анализируются все электротехнические изделия, входящие в систему автоматизации, каждое из которых имеет несколько вариантов производства их элементов, отличающихся себестоимостью изготовления и числовыми значениями показателей надежности. С помощью решения задачи на ЭВМ определяется оптимальный вариант изготовления каждого элемента по всем изделиям, входящим в систему автоматизации, а также оптимальный вариант конструкций электроизделий, который обеспечивает минимум приведенных затрат при функционировании всей системы среди всех значений исследуемого множества вариантов. В практике оптимизации показателей надежности средстз труда применяются методы целенаправленного перебора, градиентного спуска, дифференцирования модели оптимальной надежности и приравнивания к нулю полученного результата и др. Они могут быть использованы для установления экономически целесообразных показателей надежности отдельных электроизделий. [c.245]

Кроме того, можно отметить, что задачи оптимизации сетевых моделей решаются по одному варианту технологической последовательности строительства, т. е. в них не учитывается возможность изменения технологии строительства, варьирования глубины совмещения процессов и т. д. В задачах выравнивания ресурсов и корректировках по времени сетевые модели вообще приводятся к детерминированной календарной форме и теряют свои примущества динамических моделей. В детерминированных сетевых моделях, даже в обобщенных сетевых моделях, записанных в терминах событий, трудно описать с достаточной простотой сущность поточно-организационных вероятностных строительных процессов, что не позволяет разрабатывать мероприятия по обеспечению надежности строительного производства. Из-за указанных недостатков сетевые модели не нашли достаточно широкого применения в практике строительства объектов транспорта нефти и газа. [c.29]

При такой постановке задачи оптимизации плана производства НПЗ модель (2)— (9) является нелинейной. Аналогичные постановки имели место в работах [2, 3, 4,. Б]. Пути решения указанных задач в основном связываются с различными методами линеаризации, предложенными в работе Дж, Данцига 16]. Подробное обоснование этих методов в отношении моделей оптимизации плана производства НПЗ рассматривается в работах [3, 4]. Недостатками методов линеаризации является, во-первых, значительное увеличение размерности моделей, а во-вторых, усложнение подготов-.ки исходной информации для решения. [c.98]

Изложенное является результатом существующей практики создания предприятий без комплексного решения всех взаимосвязанных вопросов организации основных и обслуживающих предпрятий. Соответствие организационных решений задачам развития производства может быть обеспечено на стадии проектирования и последующей систематической работы по поддержанию этого соответствия в определенных пределах. Такой подход создает предпосылки для повышения эффективности производства за счет оптимизации организационных решений в конкретных условиях его осуществления. [c.212]

Методы линейного программирования. Первые исследования по постановке и разработке методов решения линейных оптимизационных задач были проведены в тридцатые годы Л. В. Канторовичем. В 1939 г. им была опубликована книга Математические методы организации и планирования производства , в которой впервые был ш сдложен эффективный метод решения задач оптимизации для моделей с линейными ограничениями и линейным критерием. Однако достоинство книги состояло не только в этом — в пей было показано, что модели экономических систем широкого класса могут быть достаточно точно построены на основе использования линейных соотношении. В дальнейшем эти идеи получили широкое распространение, и в настоящее время липейиые модели и методы оптимизации в таких моделях составляют основу, на которой базируется исследование прикладных экономических задач. [c.50]

Применение методов линейного программирования позволяет руководителю решать различные задачи оптимизации в условиях ограничения. Например, руководитель производства принимает решения относительно норм выпуска ряда готовых изделий, с тем чтобы максимизировать прибыль компании. Такие нормы зависят от различных условий, в частности, от наличия ресурсов и покупательс- [c.260]

Формализация задачи оптимизации календарного планирования основного производства НПП осуществляется следующим образом т tJ t-Mi0t(min 9г уг )] — >- max (3.92) [c.78]

Существует множество компьютерных программ, позволяющих отыскивать решения в задачах с десятками и даже сотнями параметров и ограничений. Рассмотренный нами в примере 2.15 случай представлял собой задачу оптимизации выпуска при двухпродуктовом производстве (марки А и В). Реальные же предприятия в подавляющем большинстве случаев выпускают гораздо более широкую номенклатуру продукции, вовлекая при этом в производство не два, как в примере 2.15 (1-й и 2-й сорта), а сотни и тысячи видов различных ресурсов. Ограничения могут касаться не только технологических и финансовых возможностей предприятия (т.е. характеристик производства «на входе»), но и особенностей получаемых отходов и побочных продуктов, уровня загрязнения окружающей среды с учетом действующего экологического законодательства и других факторов (т.е. характеристик производства «на выходе»). В отдельных случаях весьма существенными оказываются ограничения по времени, например, если предприятие испытывает сложности с поставками сырья в определенные периоды в течение года. [c.110]