О2 это что: Кислород — Википедия – O2 — Кислород | Химия соединений

Витамин B2 (Рибофлавин) — влияние на организм, польза и вред, описание

Общая характеристика витамина В2 (Рибофлавина)

Рибофлавин был выведен из группы витаминов В, в 1933 году, в качестве устойчивого к высоким температурам элемента, из окрашенного в жёлтый цвет вещества.

Рибофлавин называют «витамином красоты», так как от нормальной концентрации этого вещества в нашем организме зависит состояние кожи, ногтей и волос.

Витамин B2 (рибофлавин, лактофлавин) – один из наиболее важных водорастворимых витаминов. Зарегистрирован в качестве пищевой добавки E101.

Физико-химические свойства витамина В2

В2 представляет собой игольчатые кристаллы жёлто-оранжевого цвета, собранные в большие колбы, имеет горький вкус. Рибофлавин стабилен в кислотной и быстро разрушается в щелочной среде. Хорошо переносит нагревание.

Рибофлавин является биологически активным веществом, играющим важную роль в поддержании здоровья человека (калоризатор). Биологическая роль рибофлавина определяется вхождением его производных – коферментов – в состав большого числа важнейших окислительно-восстановительных ферментов.

Пищевые источники витамина В2

Продукты с наибольшим содержанием витамина B2: печень (3,5 мг на 100 г продукта) и почки (3,5 мг), яйца (0,3 мг), миндаль (0,8 мг), грибы (0,4 мг), творог (0,3 мг), гречневая крупа (0,2 мг), молоко (0,15 мг), мясо (0,29 мг), дрожжи (3 мг).

Суточная потребность в витамине В2

Рекомендуемая суточная потребность в витамине В2 в мг в зависимости от возраста составляет:

Возраст/пол	Суточная норма витамина (в мг)
Дети 1-6 месяцев	0,5
Дети 7-12 месяцев	0,8
Дети 1-3 лет	0,9
Дети 3-7 лет	1,2
Дети 7-10 лет	1,5
Подростки 10-14 лет	1,6
Юноши 15-18 лет	1,8
Мужчины 19-59 лет	1,5
Мужчины 60-74 лет	1,7
Мужчины старше 75 лет	1,6
Девушки 15-18 лет	1,5
Женщины 19-59 лет	1,3
Женщины 60-74 лет	1,5
Женщины старше 75 лет	1,4
Беременные женщины	2,0
Кормящие женщины	2,2

Снижению уровня витамина В2 в организме способствуют: погодные условия, большие психологические и физические нагрузки, прием оральных контрацептивов, плохая работа щитовидной железы, чрезмерное употребление алкоголя.

Полезные свойства витамина В2

Витамин B2 необходим для образования эритроцитов, антител, для регуляции роста и репродуктивных функций в организме. Он также необходим для здоровой кожи, ногтей, роста волос и в целом для здоровья всего организма, включая функцию щитовидной железы.

Важнейшие функции витамина В2:

• Участвует в углеводном, белковом и жировом обмене;
• Участвует в синтезе гликогена;


• Помогает усвоить железо, необходимое для создания новых красных кровяных телец;
• Укрепляет иммунитет и защитные механизмы организма;
• Играет важную роль в работе нервной системы, помогает при лечении таких болезней как: эпилепсия, болезнь Альцгеймера и повышенной тревожности;
• Необходим для сохранения нормального состояния слизистых оболочек полости рта и кишечника;
• Регулирует функцию щитовидной железы;
• Способствует нормальному световому и цветовому зрению, защищает сетчатку глаза от избыточного воздействия ультрафиолетовых лучей, уменьшает утомляемость глаз, обеспечивает адаптацию к темноте, повышает остроту зрения и играет большую роль в предотвращении катаракты;
• Помогает при угревой сыпи, дерматите, экземе;
• Ускоряет заживление поврежденных тканей;
• Уменьшает воздействие токсинов на легкие и дыхательные пути.

Вредные свойства витамина В2

Вредное свойство у витамина В2 только одно – возможное ожирение печени. Но это может произойти лишь в случае поглощения витаминных комплексов в неконтролируемых режимах и злоупотреблениями различными БАДами.

Усвояемость витамина В2

Витамин В2 достаточно хорошо усваивается из пищи, однако у него есть некоторые особенности. Из овощей он всасывается лучше, если они перед этим подвергаются термической обработке. Люди, применяющие В2 в виде пищевой добавки, должны помнить, что витамин хорошо усваивается тогда, когда в желудке присутствует достаточно пищи. Если принимать натощак, рибофлавин усвоится хуже. Также, если человек сидит на строгой диете и ест совсем помалу, это снижает усвояемость В2.

Дефицит витамина В2 в организме

Внешними проявлениями недостаточности рибофлавина у человека являются поражения слизистой оболочки губ с вертикальными трещинами и слущиванием эпителия, изъязвления в углах рта, отёк и покраснение языка, себорейный дерматит на носогубной складке, крыльях носа, ушах, веках. Часто развиваются также изменения со стороны органов зрения: светобоязнь, васкуляризация роговой оболочки, конъюнктивит, кератит и в некоторых случаях – катаракта (calorizator). В ряде случаев при авитаминозе имеют место анемия и нервные расстройства, проявляющиеся в мышечной слабости, жгучих болях в ногах и др.

Основные причины недостатка рибофлавина у человека – недостаточное потребление молока и молочных продуктов, являющихся главными источниками этого витамина; хронические заболевания желудочно-кишечного тракта, приём медикаментов являющихся антагонистами рибофлавина.

Избыток витамина В2 в организме

Человеческий организм не накапливает рибофлавин, и любой избыток выводится вместе с мочой. При избытке рибофлавина моча окрашивается в ярко-жёлтый цвет. Признаки избытка витамина В2: нарушение усвоения железа, повышение сухожильных рефлексов, церебральная недостаточность, головокружение, редко зуд, онемение, чувство жжения или покалывания.

Взаимодействие витамина В2 (Рибофлавина) с другими веществами

Витамин В2 совместно с фолиевой кислотой (витамином В9) участвует в процессе создания новых кровяных телец в костном мозге, содействует синтезу эритропоэтина (главного стимулятора кроветворения).

Вместе с витамином В1 рибофлавин способствует поддержанию уровня железа в крови.

В2 способствует активации витаминов В6 (пиридоксина), В9 (фолиевой кислоты) и витамина К (филлохинона).

Больше о витамине В2 смотрите в видео-ролике «Органическая химия. Витамин В2»

Автор: Марина Л. (специально для Calorizator.ru)
Копирование данной статьи целиком или частично запрещено.

Tele2 — Википедия

Эта статья — о международной компании Tele2. О Tele2 в России см. Tele2 Россия.

Tele2 AB — международная телекоммуникационная компания. Штаб-квартира компании находится в Стокгольме.

Компания была основана в конце 1970-х как дочернее предприятие группы компаний Investment AB Kinnevik^[en] (Швеция). В то время она называлась Comvik^[1]

. В 1988 году компания получила лицензию на оказание услуг мобильной связи в формате GSM и четырьмя годами позже запустила свою первую сеть в Швеции. В 1993 году появилось современное название — Tele2^[1].

В 1996 году компания начала экспансию за пределы Швеции, с 1997 по 2004 годы развернув сети в Норвегии, Эстонии, Литве, Германии, Австрии, Швейцарии, Нидерландах, Латвии и в других странах Европы. В 2000 году компания получила первые 3G-лицензии^[1], в 2014 году начала строительство сетей 4G. В 2003 году Tele2 запустила сети мобильной связи в России, с 2010 года начала работу в Казахстане.

14 декабря 2018 года Tele2 вводит систему цифровых дисплеев, которыми можно управлять из офиса компании. Эта технология позволяет отображать актуальную и полную информацию об ассортименте салонов в режиме реального времени^[2].

Крупнейший акционер компании — Investment AB Kinnevik (30,1 % голосующих акций), остальные акции находятся в свободном обращении

[3].

Информация в этой статье или некоторых её разделах устарела. Вы можете помочь проекту, обновив её и убрав после этого данный шаблон.

Холдинг Tele2 по состоянию на 2010 год работал в 11^[4] странах мира: Швеции, Норвегии, Нидерландах, Германии, Австрии, Хорватии, Эстонии, Латвии, Литве, России и Казахстане, оказывая услуги мобильной и фиксированной связи, интернет-доступа и кабельного ТВ 30 миллионам клиентов^[5]. На лицензионной территории Tele2 проживает более 61 миллиона человек. Рыночная стратегия — сотовый дискаунтер.

Совокупная выручка компании за 2010 год составила $6,4 млрд (рост по сравнению с 2009 годом на 1,8 %), чистая прибыль — $1,07 млрд^[5]

.
В октябре 2007 года стало известно, что компания Tele2 продала свои подразделения в Испании и Италии компании Vodafone за 775 млн евро^[6].

В марте 2011 года компания Tele2 объявила сроки запуска своих операций в Республике Казахстан. Сеть сотовой связи Tele2 начала работу в Актюбинской области 24 апреля. В мае-июне 2011 года в территорию покрытия Tele2 вошли Уральск, Алматы, Шымкент и Астана с окружающими их территориями^[7].

К концу 2018 года общее число абонентов Tele2 достигло 42, 3 млн человек^[8].

«Tele2» в России[править | править код]

«Tele2» до момента продажи российского бизнеса в 2013 году являлась единственной иностранной компанией, которая достаточно успешно действовала на российском сотовом рынке, хотя так и не смогла получить лицензию на связь 3G^[3]. В марте 2012 года «Tele2» провела тестовые испытания 4G в Пскове и Омске. Таким образом, была доказана совместимость 2G—4G (в обход 3G)^[9]. По состоянию на начало июля 2013 года, «Tele2» являлась четвёртым по числу абонентов оператором сотовой связи в России: абонентская база в стране на это время составляла 23,2 млн человек

[10]. Для «Tele2» Россия была основным рынком, обеспечивавшим на 2010 год свыше половины всех абонентов и 34,7 % (наибольшая доля среди всех стран) EBITDA^[5].

27 марта 2013 года стало известно, что шведская группа Tele2 приняла решение о продаже российского подразделения группе ВТБ^[11]. 4 апреля сделка была завершена^[12][13].

17 октября 2013 года Группа ВТБ продала 50 % акций компании «Tele2 Россия» консорциуму частных инвесторов, владеющих Банком «Россия», среди которых Юрий Ковальчук (председатель совета директоров Банка «Россия») и Алексей Мордашов (совладелец «Северстали»), а также 5 % компании «Tele2 Россия» купила страховая группа «СОГАЗ»^[14][15][16].

В 2014 году «Ростелеком» и «Tele2 Россия» создали совместное предприятие (СП) «T2 Рус Холдинг», интегрировав свои мобильные активы. «Ростелеком» стал участником совместного предприятия с долей в уставном капитале в размере 45 % в голосах и 45 % экономической доли. Таким образом был создан новый федеральный оператор мобильной связи, владеющий широким спектром лицензий и частот по всей стране (в том числе 3G и федеральной LTE), текущим географическим присутствием в 64 регионах, существенной 16 % долей на рынке сотовой связи России, которую обеспечивают более 38 млн сотовых абонентов

[17].

В 2015 году «Tele2 Россия» провела юридическую реорганизацию, слив все региональные сотовые активы (кроме ЗАО «АКОС», Владивосток) в ООО «Т2 Мобайл». «T2 Рус Холдинг», переименованное в ООО «Т2 РТК Холдинг», является головной компанией группы, а его 100%-ная «дочка» «Т2 Мобайл» осуществляет операционную деятельность, оказывая услуги сотовой связи под брендом Tele2^[18].

Российские сотовые операторы продолжают готовиться к внедрению виртуальных сим-карт eSIM. Tele2 вместе с «Ростелекомом» протестирует возможность переноса абонентского номера при подключении по этой технологии.^[19]

Tele2 в других странах[править | править код]

Tele2 в Казахстане[править | править код]

В декабре 2009 компания подписала контракт о приобретении 51 % акций казахстанского сотового оператора «Мобайл Телеком-Сервис» (МТС) у государственного оператора фиксированной связи Казахтелеком (сделка была завершена в марте 2010 года^[20]). Сумма сделки составила 545 млн шведских крон ($76,7 млн) с обязательством инвестировать в оператора 360 млн крон ($50,6 млн). Tele2 также получил опцион на выкуп в течение 5 лет оставшихся 49 % акций МТС, принадлежащих частной компании Amun Capital^[17].
В апреле 2011 года Tele2 осуществил запуск сети сотовой связи в Актюбинской области, после чего оператор стал работать во всех регионах Казахстана^[18].

В 2015 году Tele2 объявил о создании совместного предприятия с крупнейшим оператором фиксированной связи Казахтелеком. В начале марта 2016 года Tele2 Казахстан и АО «Казахтелеком» сообщили о слиянии своих компаний^[21]. В итоге Tele2 и Казахтелеком будут владеть 51 % и 49 % голосующих акций и 49 % и 51 % обыкновенных акций в совместном предприятии, соответственно. Tele2 сохранит контроль над управлением совместным предприятием. Пиетари Кивикко был назначен председателем правления совместного предприятия Altel и Tele2 Казахстан^[22], но, после его ухода из Tele2 Казахстан СП возглавил новый СЕО — Роман Володин^[23]. Благодаря слиянию Tele2 Kazakhstan получила доступ к лицензии для строительства 4G с неограниченным интернет-доступом для абонентов.^[24] В марте 2016 года Tele2 Казахстан объявила о коммерческом запуске LTE по всей территории Казахстана.

По итогам 2015 года, доля оператора на рынке Казахстана составила 20 %.

1 июля 2019 года Tele2 обьявил официальный уход с Казахстанского рынка сотовой связи
^[23].

Что означает 2 в h3O? Именно цифра 2

2 атома водорода и 1 атом кислорода — химическая формула воды.

2 атомо водорода и 1 атом кислорода

это индекс. Она показывает число атомов в формуле. В данном случае означает 2 атома водорода (Н) а у кислорода (О) нету индекса это означает что у него 1 атом

Молекула воды состоит из 3 атомов, из них 2 обозначает количество атомов водорода и 1 атом кислорода. Эти цифры называются индекс и обозначают количество атомов в молекуле

2 атома водорода.

H-ЭТО КИСЛОРОД! 2O-ЭТО ВОДОРОД!!! ГЛУПЫЕ

О большое: что это такое, почему это важно, и почему это не важно.

Очень интересная статья Shen Huang о нотации О большое: Big O notation: why it matters, and why it doesn’t
В статье присутствует математические формулы, формальные определения, математические доказательства и т.п. При переводе возможно были допущены не точности в этих понятиях. Но тем не менее статья очень интересна для получения базовых знаний, о том что такое нотации Большое О, зачем оно нужно и какие бывают варианты нотаций.

Вы действительно понимаете что такое О большое (Big O)? Если это так, то эта статья поможет вам освежить ваши знания перед собеседованием. Если нет, эта статья расскажет вам о том что это такое и зачем нужно об этом знать.

Нотация О большое является одним из самых фундаментальных инструментов анализа сложности алгоритма. Эта статья написана с предположением, что вы уже являетесь программистом и за вашими плечами большое количество написанного кода. Кроме того, для лучшего понимания материала потребуется знания основ математики средней школы. И так если вы готовы, давайте начнем!

Picture of a Mandelbrot set, which relates to Complex Numbers and Recursions, Pixabay

Содержание

1. Что такое нотация О большое и почему это важно
2. Формальное определение обозначения О большое
3. О большое (Big O), О малое (Little O), Омега (Omega) и Тета (Theta)
4. Сравнение сложности между всеми нотациями
5. Время и пространство сложности
6. Лучшая, Средняя, Худшая, Ожидаемая Сложность
7. Почему О большое может быть не важна
8. Заключение…

1. Что такое нотация О большое и почему оно важно

«Нотация О большое – это математическая нотация, которая описывает ограничивающее поведение функции, когда аргумент стремится к определенному значению или бесконечности. Он является членом семейства нотаций, изобретенных Полом Бахманом, Эдмундом Ландау и другими, которые в совокупности называются нотациями Бахмана-Ландау или асимптотическими нотациями ».

Проще говоря, нотация О большое описывает сложность вашего кода с использованием алгебраических терминов.

Чтобы понять, что такое О большое, мы можем взглянуть на типичный пример O (n²), который обычно произносится как «Большой O в квадрате». Буква «n» здесь представляет размер входных данных, а функция «g (n) = n²» внутри «O ()» дает нам представление о том, насколько сложен алгоритм по отношению к количеству входных данных.

Типичным алгоритмом со сложностью O(n²) будет алгоритм сортировки выбором. Сортировка выбором – это алгоритм сортировки, который выполняет итерацию по списку, чтобы гарантировать, что каждый элемент с индексом i является i-м наименьшим/наибольшим элементом списка. Наглядный пример.

Алгоритм может быть описан следующим кодом. Чтобы убедиться, что i-й элемент является i-м наименьшим элементом в списке, этот алгоритм сначала просматривает список с помощью цикла for. Затем для каждого элемента он использует другой цикл for, чтобы найти наименьший элемент в оставшейся части списка.

SelectionSort(List) {
  for(i from 0 to List.Length) {
    SmallestElement = List[i]
    for(j from i to List.Length) {
      if(SmallestElement > List[j]) {
        SmallestElement = List[j]
      }
    }
    Swap(List[i], SmallestElement)
  }
}

В этом сценарии мы рассматриваем переменную List как входные данные, поэтому размер ввода n – это количество элементов внутри List. Предположим, что оператор if, а присвоение значения, ограниченное оператором if, занимает постоянное время. Затем мы можем найти О большое для функции SelectionSort, проанализировав, сколько раз выполняются операторы.

Сначала внутренний цикл for выполняет операторы внутри n раз. А затем, после увеличения i, внутренний цикл for выполняется n-1 раз … пока он не будет запущен еще один раз, тогда оба цикла for достигнут своих условий завершения.

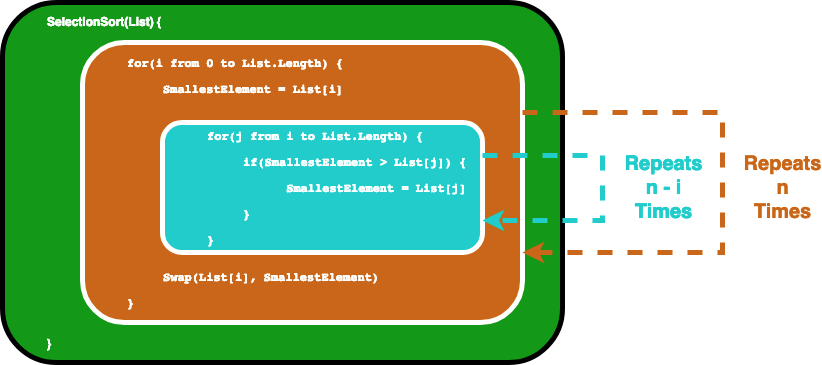Selection Sort Loops Illustrated

На самом деле это в конечном итоге дает нам геометрическую сумму, и благодаря математики средней школе мы обнаружим, что внутренний цикл будет повторяться 1 + 2… + n раз, что равно n(n-1)/2 раза. Если мы умножим это, мы получим n²/2-n/2.

Когда мы вычисляем О большое, мы заботимся только о доминирующих операторах, и не заботимся о коэффициентах. Таким образом, мы выбираем n² как О большое. Мы записываем его как O(n²), а произносим как «О большое в квадрате».

Теперь вам может быть интересно, что это за «доминирующие операторы»? И почему нас не волнуют коэффициенты? Не волнуйтесь, мы рассмотрим эти вопросы по очереди далее.

2. Формальное определение нотации О большое

Когда-то давно жил один индийский король, который захотел наградить мудреца. Мудрец попросил в качестве награды только пшеницы, которая бы заполнила все шахматную доску.

Но с определенным условием: в первой клетке должно быть 1 зернышко пшеницы, затем 2 зернышка на второй клетке, затем 4 на следующей … и так далее на каждой клетке шахматной доске должно быть вдвое больше количество зерен, чем на предыдущей. Наивный король согласился без колебаний, думая, что это слишком простое условие…

Wheat and Chess Board, Image from Wikipedia

Так сколько зерна пшеницы должен царь мудрецу? Мы знаем, что шахматная доска имеет 8 квадратов на 8 квадратов, что в сумме составляет 64 фишки, поэтому в итоговой фишке должно быть 2⁶⁴ зерна пшеницы. Если вы проведете самостоятельный расчет, вы получите 1,8446744 * 10¹⁹, то есть около 18, за которыми следуют 18 нулей. Предполагая, что каждое зерно пшеницы весит 0,01 грамма, это дает нам 184 467 440 737 тонн пшеницы. А 184 миллиарда тонн – это много, не правда ли?

Числа могут расти довольно быстро, не так ли? Та же логика относится и к компьютерным алгоритмам. Если требуемые усилия для выполнения задачи растут экспоненциально по отношению к размеру входных данных, алгоритм может в конечном итоге стать чрезвычайно затратным.

Если вы продолжите удвоение 2⁶⁴, то результат будет быстро потерян за пределами значащих цифр. Вот почему, когда мы смотрим на темпы роста, мы заботимся только о доминирующих операторах. И поскольку мы хотим проанализировать рост по отношению к размеру ввода, коэффициенты, которые только умножают число, и не растут с размером ввода, не содержат никакой полезной информации.

Ниже приведено формальное определение Большого O:

CSE 373 Slides from University of Washington

Формальное определение полезно, когда вам нужно выполнить математическое доказательство. Например, сложность для сортировки выбором может быть определена функцией f (n) = n²/2-n/2, как мы обсуждали в предыдущем разделе.

Если мы допустим, чтобы наша функция g(n) была n², мы можем найти константу c = 1 и N₀ = 0, при условии, N > N₀, где N² всегда будет больше, чем N²/2-N/2. Мы можем легко доказать это, вычитая N²/2 из обеих функций, тогда мы можем видеть, что N²/2 > -N/2 будет истинно, когда N>0. Поэтому мы можем прийти к выводу, что f(n) = O (n²), в другом порядке выбора это «О большое квадрат».

Вы могли заметить небольшую хитрость. То есть, если вы заставите g(n) расти быстрее, чем что-либо другое, O(g(n)) всегда будет достаточно большим. Например, для любой полиномиальной функции вы всегда будете правы, говоря, что оно являются O(2ⁿ), потому что 2ⁿ в конечном итоге будет всегда больше любого полинома.

С математической точки зрения вы будете правы, но обычно, когда мы говорим о Большом O, нам нужно знать жесткую границу (tight bound) функции. Вы узнаете об этом больше, в следующем раздел.

Но прежде чем мы пойдем дальше, давайте проверим ваше понимание следующим вопросом. Ответ будет приведен в следующем разделе.

Вопрос: Допустим изображение представлено двумерным массивом пикселей. Вы используете вложенный цикл for для итерации по каждому пикселю (то есть у вас есть цикл for, проходящий по всем столбцам, и другой цикл внутри, чтобы пройти по всем строкам). Какая в этом случае будет сложность алгоритма?

3. О большое, O малое, Омега и Тета

Ниже приведены формальные математические определения этих нотаций:

О большое: «f(n) есть O(g (n))» тогда и только тогда, когда некоторые константы c и N₀, f(N) ≤ cg(N) для всех N> N₀

Малое O: «f(n) есть o (g(n))», если f(n) есть O(g(n)) и f(n) не есть Θ(g(n))

Омега: «f(n) есть Ω(g(n))» тогда и только тогда, когда некоторые константы c и N₀, f(N) ≥ cg(N) для всех N> N₀

Тета: «f (n) есть Θ(g (n))» тогда и только тогда, когда f(n) есть O(g(n)), а f(n) есть Ω(g(n))

Простыми словами:

• О большое (O()) описывает верхнюю границу сложности.
• Малое O (o()) описывает верхнюю границу, исключая точную оценку.
• Омега (Ω ()) описывает нижнюю границу сложности.
• Тета (Θ ()) описывает точную оценку сложности.

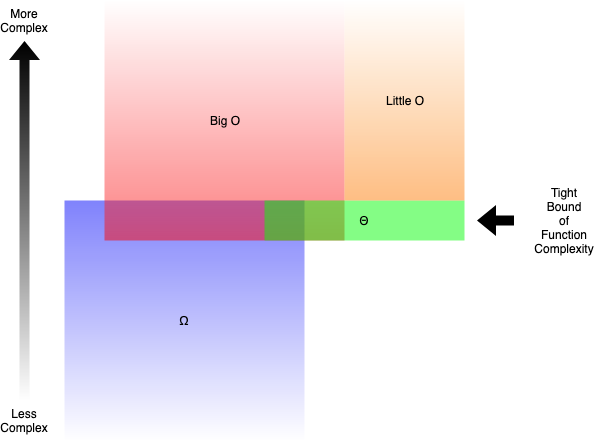Relationships between Big O, Little O, Omega & Theta Illustrated

Например, функция g(n) = n² + 3n – это O(n³), o(n⁴), Θ(n²) и Ω (n). Но вы все равно были бы правы, если бы сказали, что это Ω(n²) или O(n²).

Вообще, когда мы говорим о Большом O, мы на самом деле имеем в виду Тета (Θ Theta). Бессмысленно, когда вы определяете верхнюю границу, намного превышающую объем анализа. Это было бы похоже на решение неравенств путем помещения ∞ на большую сторону, что почти всегда формально сделает вас правым.

Но как определить, какие функции сложнее других?

4. Сравнение сложности между типичными нотациями Больших O

Когда мы пытаемся выяснить О большое для конкретной функции g(n), мы заботимся только о доминирующем операторе (dominant term) функции. Доминирующий оператор – это такой оператор, который растет быстрее всего.

Например, n² растет быстрее, чем n, поэтому, если у нас есть что-то вроде g(n) = n² + 5n + 6, то О большое будет (n²). Если вы когда нибудь проводили некоторые исчисления, это очень похоже на сокращение пределов для дробных многочленов, когда вам важен только доминирующий оператор для числителей и знаменателей в конце.

Another way to look at Big O, Image from Stack Overflow

Но какая функция растет быстрее, чем другие? На самом деле существует довольно много правил.

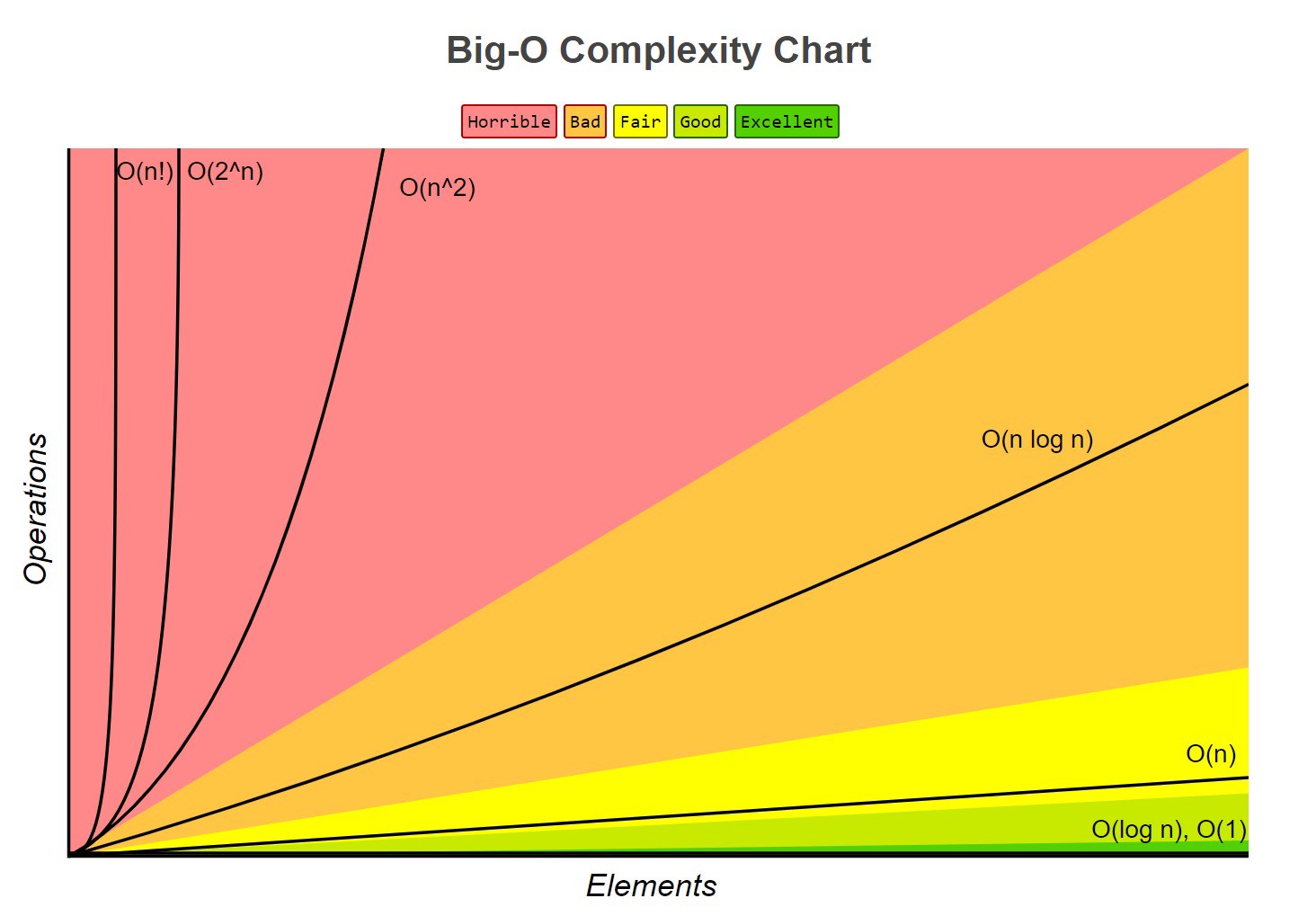Complexity Growth Illustration from Big O Cheatsheet

1. O(1) имеет наименьшую сложность

Часто называемый «постоянный по времени», если вы можете создать алгоритм для решения проблемы с O(1), то это будет лучший выбор алгоритма. В некоторых сценариях сложность может выходить за пределы O(1), тогда мы можем проанализировать их, найдя ее аналог O(1/g(n)). Например, O(1/n) является более сложным, чем O(1/n²).

2. O (log(n)) является более сложным, чем O(1), но менее сложным, чем полиномы

Поскольку сложность часто связана с алгоритмами «разделяй и властвуй», O (log(n)) – это, как правило, хорошая сложность, которую можно достичь для алгоритмов сортировки. O (log(n)) является менее сложным, чем O (√n), потому что функцию квадратного корня можно считать полиномом, где показатель степени равен 0,5.

3. Сложность многочленов увеличивается с ростом степени

Например, O (n⁵) является более сложным, чем O (n⁴).

4. Экспоненты имеют большую сложность, чем полиномы, если коэффициенты положительные кратные n

O (2ⁿ) является более сложным, чем O (n⁹⁹), но O (2ⁿ) на самом деле является менее сложным, чем O(1). Обычно мы берем 2 в качестве основы для степеней и логарифмов, потому что в компьютерных науках все имеет тенденцию быть двоичным, но степень можно изменить, изменив коэффициенты. Если не указано иное, основание для логарифмов принимается равным 2.

5. Факториалы имеют большую сложность, чем степень

Если вам интересны доказательства, посмотрите Гамма-функцию (Gamma function), это аналитическое продолжение факториала. Краткое доказательство состоит в том, что и факториалы, и степень имеют одинаковое количество умножений, но числа, которые умножаются, растут для факториалов, оставаясь неизменными для степени.

6. Умножение

При умножении сложность будет больше, чем оригинал, но не больше, чем эквивалентность умножения чего-то более сложного. Например, O (n*log (n)) является более сложным, чем O (n), но менее сложным, чем O (n²), потому что O (n²) = O (n * n), а n более сложный, чем log (n). ).

Если хотите можете проверить свое понимание. Попробуйте ранжировать следующие функции от самых сложных до менее. Решения с подробными объяснениями можно будет найти в следующем разделе. Некоторые из них достаточно сложные и могут потребовать более глубокого понимания математики. Когда вы доберетесь до решения, вы узнаете об этом больше.

Вопрос: Расставьте следующие функции от самых сложных до менее.

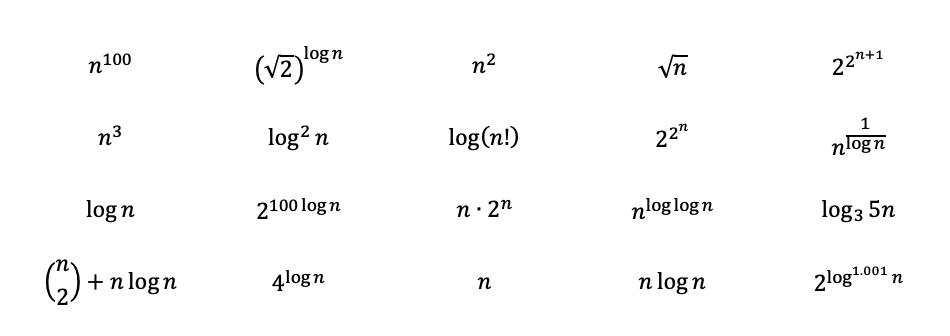Examples taken from Textbook Problems

Решение для вопроса из Раздела 2:

На самом деле это был вопрос с подвохом, чтобы проверить ваше понимание. Возможно вы бы предположили что ответ равен O (n²), потому что есть вложенный цикл for. Но нужно понять, что входными данными является массив изображений, и каждый пиксель в алгоритме проходится только один раз, то ответ на самом деле будет O (n). В следующем разделе будут рассмотрены другие примеры, подобные этому.

5. Время и пространство сложности

До сих пор мы обсуждали только временную сложность алгоритмов. То есть мы заботимся только о том, сколько времени потребуется программе для выполнения задачи. Что также важно, так это место, занимаемое программой в памяти для выполнения задачи. Сложность пространства связана с тем, сколько памяти будет использовать программа, и, следовательно, также является важным фактором для анализа.

Пространственная сложность работает аналогично временной сложности. Например, сортировка выбором имеет пространственную сложность O(1), потому что она хранит только одно минимальное значение и свой индекс для сравнения, максимальное используемое пространство не увеличивается с размером ввода.

Некоторые алгоритмы, такие как блочная сортировка, имеют пространственную сложность O (n), но при этом в ней можно уменьшить временную сложность до O (1). Блочная сортировка это такая сортировка в котором сортируемые элементы распределяются между конечным числом отдельных блоков (карманов, корзин) так, чтобы все элементы в каждом следующем по порядку блоке были всегда больше (или меньше), чем в предыдущем. Каждый блок затем сортируется отдельно, либо рекурсивно тем же методом, либо другим. Затем элементы помещаются обратно в массив. 

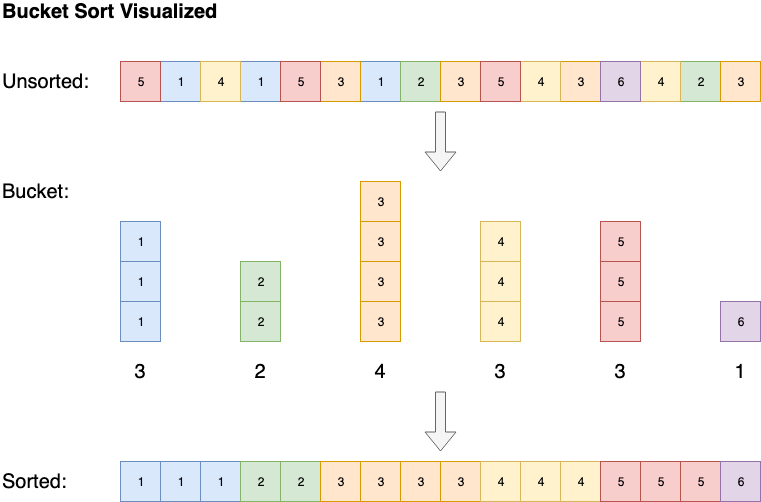Bucket Sort Visualization

6. Лучшая, Средняя, Худшая, Ожидаемая Сложность

Сложность также может быть проанализирована как лучший случай, наихудший случай, средний случай и ожидаемый случай.

Для примера давайте рассмотрим сортировку вставками (insertion sort). Сортировка вставками выполняет итерацию по всем элементам в списке. Если элемент больше, чем его предыдущий элемент, он вставляет элемент назад, пока он не станет больше, чем предыдущий элемент.

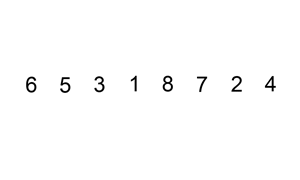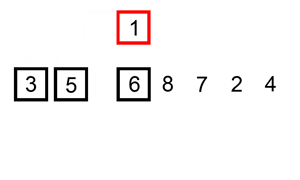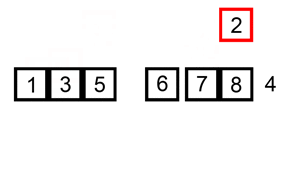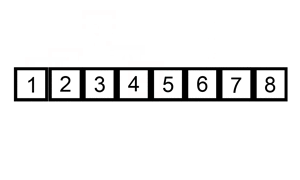Insertion Sort Illustrated, Image from Wikipedia

Если массив изначально отсортирован, обмен вообще не будет произведен. Алгоритм будет просто пройдет итерацию по массиву один раз, что приведет к временной сложности O (n). Следовательно, мы бы сказали, что наилучшая временная сложность сортировки вставками – O (n). Сложность O (n) также часто называют линейной сложностью.

Иногда алгоритму может просто не повезти. Например, быстрая сортировка будет должна пройти через список за O (n), если элементы отсортированы в обратном порядке, но в среднем этот алгорит сортирует массив за O (n * log(n)). Как правило, когда мы оцениваем временную сложность алгоритма, мы смотрим на ее худшую производительность. Подробнее об этом и быстрой сортировке мы поговорим в следующем разделе.

Средняя сложность описывает ожидаемую производительность алгоритма. Иногда включает в себя расчет вероятности каждого сценария. Ниже приведена шпаргалка по временной и пространственной сложности типичных алгоритмов.

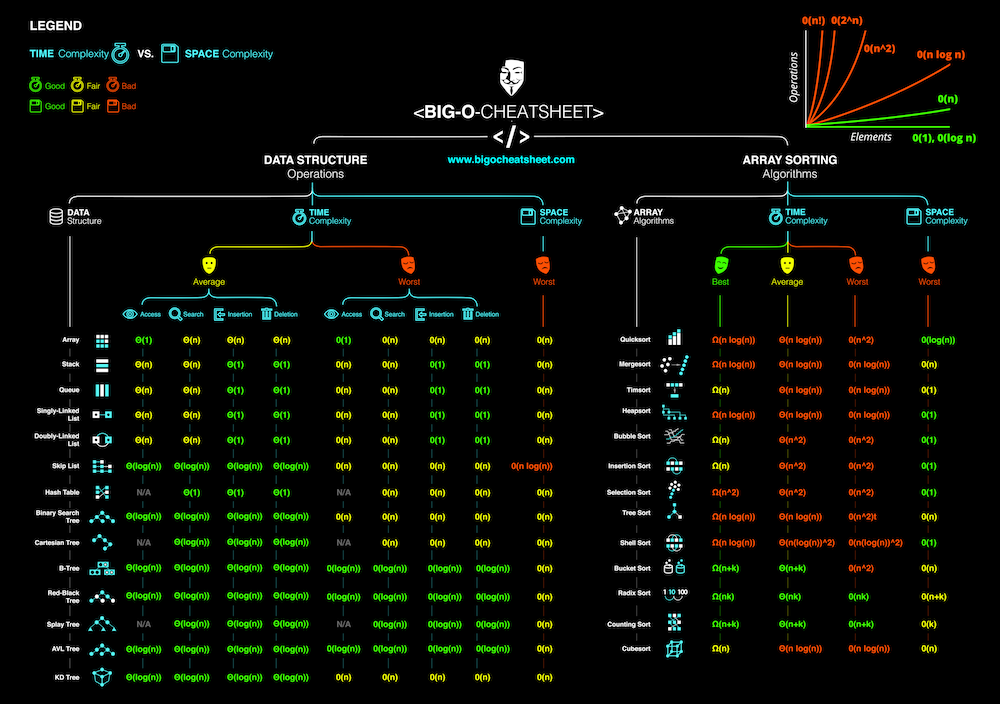Big O Cheatsheet for Common Algorithms

Решение для вопроса из Раздела 4:

Осматривая функции, мы можем начать с ранжирования следующих полиномов от наиболее сложного до менее по правилу 3. Где корень квадратный из n равен просто n в степени 0,5.

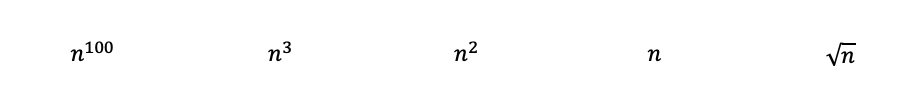
Тогда, применяя правила 2 и 6, мы получим следующее. Логарифм с основанием 3 может быть преобразован в с основанием 2 (log base conversions). Логарифм с основанием 3 по-прежнему растет немного медленнее, чем с основанием 2, и поэтому в рейтинге получает место после него.

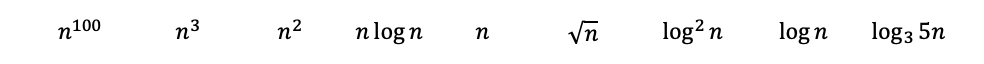
Остальные могут показаться немного сложными, но давайте попробуем быть немного повнимательнее и посмотреть, как же все такие их можно расположить.

Прежде всего, 2 в степени 2 в степени n больше 2 в степени n, а +1 еще больше его увеличивает.

Чтобы степень log (n) с основанием 2 была равна n, мы можем преобразовать следующее. Логарифм от 0,001 растет немного больше, чем просто константы, но меньше, чем почти все остальное.

Выражение, у которого n в степени log (log (n)), на самом деле является вариацией квазиполинома (quasi-polynomial), который больше полинома, но меньше экспоненты. Поскольку log (n) растет медленнее, чем n, его сложность немного меньше. Выражение с обратным логарифмом сходится к константе, поскольку 1 / log (n) расходится к бесконечности.

Факториалы могут быть представлены умножением и, следовательно, могут быть преобразованы в сложения вне логарифмической функции. «N select 2» может быть преобразовано в полином с кубическим членом, являющимся наибольшим.

И, наконец, мы можем ранжировать функции от самых сложных до наименее сложных.

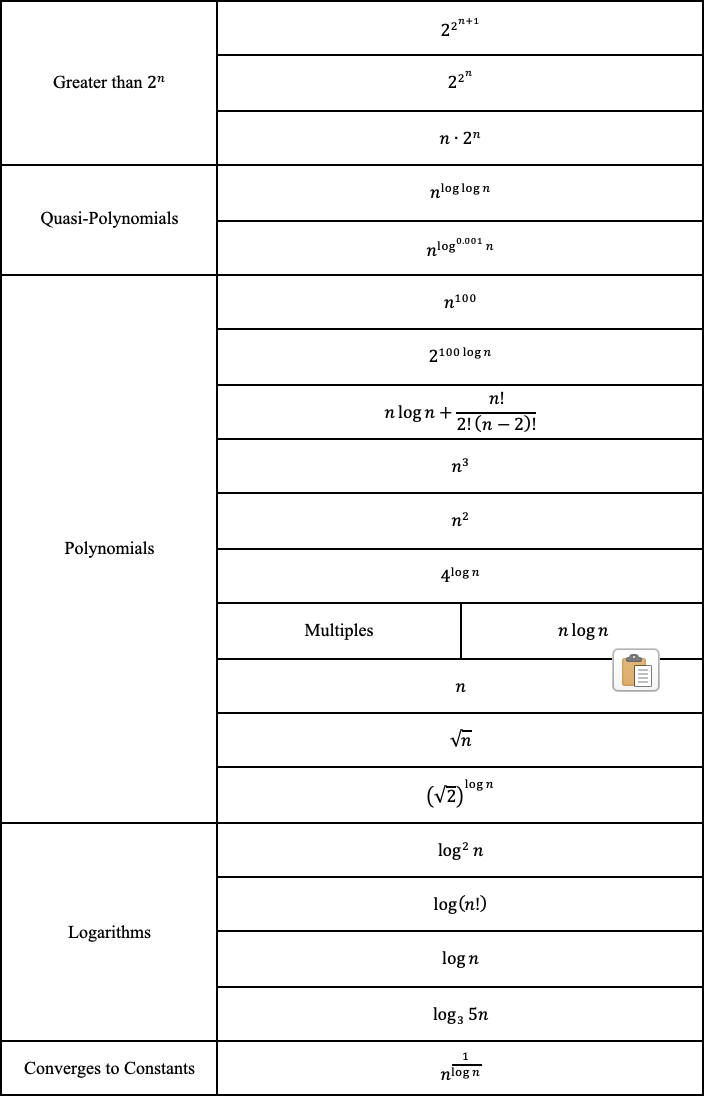
Почему О большое может не имеет значения

!!! — WARNING — !!!

Идея, обсуждаемая далее, обычно не принимается большинством программистов в мире. Озвучивайте ее при собеседованиях на свой страх и риск. Бывали случаи когда, люди провалили собеседование в Google, потому что они подвергли сомнению необходимости нотаций.

!!! — WARNING — !!!

Поскольку ранее мы узнали, что сложность по времени в наихудшем случае для быстрой сортировки будет O (n²), а для сортировки слиянием (merge sort) будет O (n * log (n)), то сортировка слиянием должна быть быстрее, верно? Ну, вы, наверное, догадались, что ответ неверен. Чтобы это продемонстрировать, я выложил этот пример сюда trinket.io. Он сравнивает время для быстрой сортировки (quick sort) и сортировки слиянием (merge sort). Мне удалось протестировать его только на массивах длиной до 10000 значений, но, как вы можете видеть, время сортировки слиянием растет быстрее, чем быстрой сортировки. Несмотря на быструю сортировку, имеющую худшую сложность O (n²), вероятность этого действительно низка. Когда дело доходит до увеличения скорости, быстрая сортировка имеет более высокую скорость чем сортировка слиянием, ограниченная сложностью O (n * log (n)), быстрая сортировка заканчивается в среднем с лучшей производительностью.

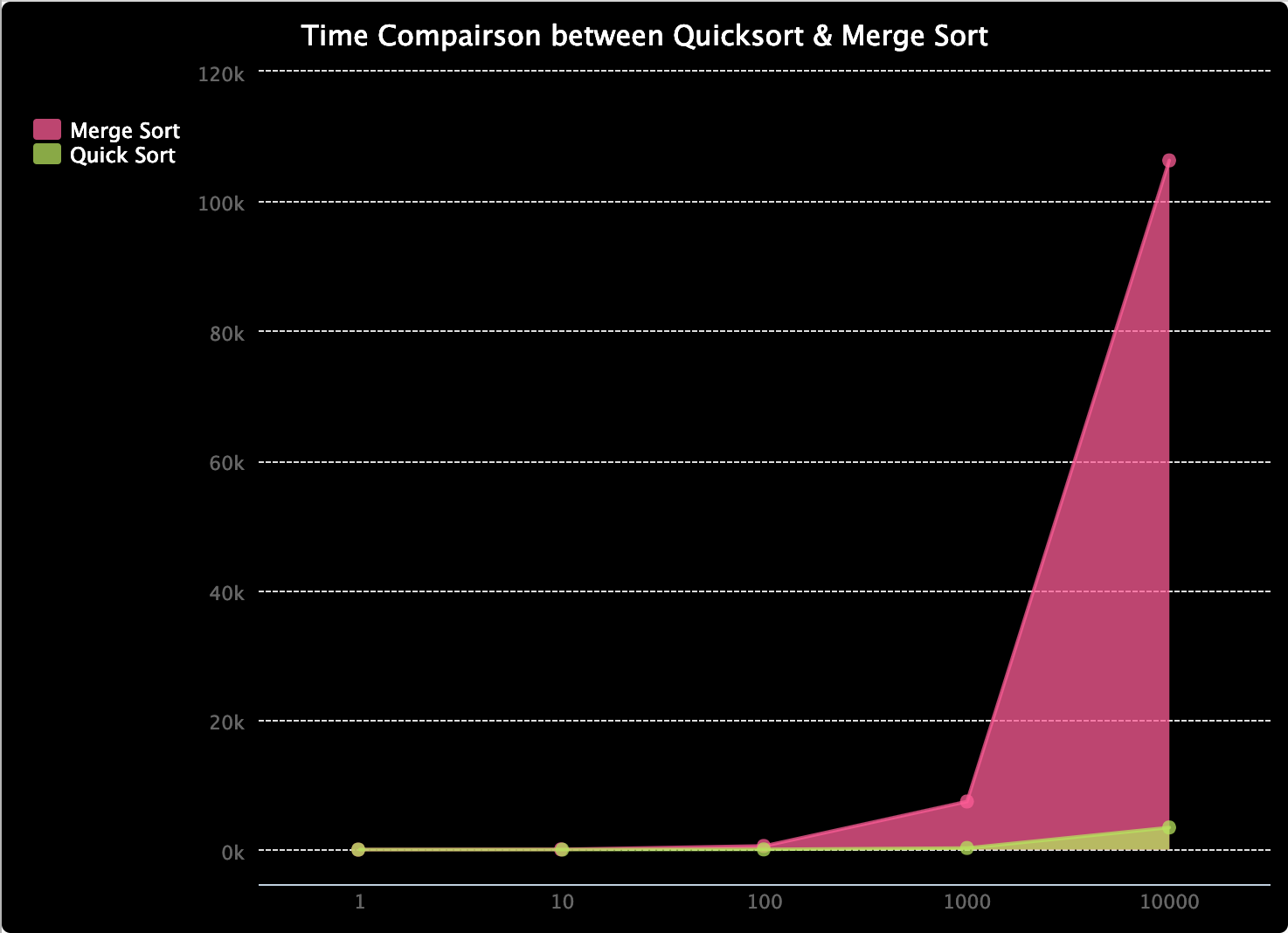
Я также сделал график, чтобы сравнить соотношение между временем, которое они занимают, так как это время трудно увидеть при более низких значениях. И, как вы можете видеть, процент времени, требуемый для быстрой сортировки, очень быстро уменьшается.

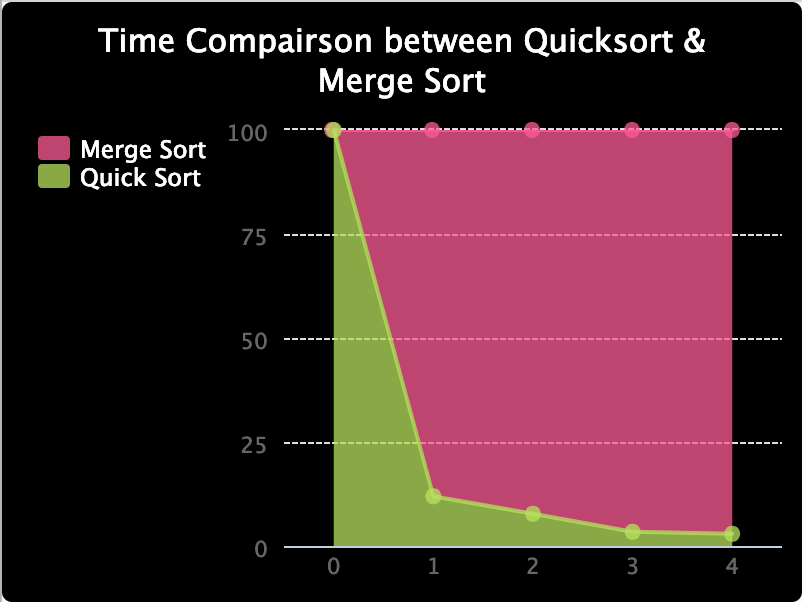
Мораль этой истории в том, что нотация О большое – это всего лишь математический анализ, который дает представление о ресурсах, потребляемых алгоритмом. Практически результаты могут быть разными. Но, как правило, это хорошая практика – пытаться снизить сложность наших алгоритмов.

Заключение…

Мне нравится кодить, изучать новые вещи и делиться ими с сообществом. Если есть что-то, что вас особенно интересует, пожалуйста, дайте мне знать. Я обычно пишу о веб-дизайне, архитектуре программного обеспечения, математике и науке о данных. Вы можете найти несколько замечательных статей, которые я написал ранее, если вас интересует какая-либо из вышеперечисленных тем.

Была ли вам полезна эта статья?

[5 / 4.2]

Дом 2 последние новости и слухи на 6 дней раньше эфира – Шлок

Schlock.ru:
свежие серии и живое общение, новости и сплетни и интервью с персонажами. Шлок не фан. клуб или антифаны,
а эксклюзивный коллективный блог. Резонный вопрос:
почему события, которые опубликованы здесь, ещё не освещались по телеканалу
«ТНТ»? Эфиры идут с задержкой
в 6 дней, а участники проекта, имея доступ в интернет, размещают на личных страничках в соцсетях подробности
с площадок телепроекта. Эти подробности моментально становятся достоянием общественности, вызывая жаркие дебаты
в сообществах. Если хотите держать руку на пульсе, узнавая новости и слухи на 6 дней раньше трансляций,
тогда наш сайт будет интересен.

Дом 2 новости и слухи на 6 дней раньше

Дом 2 новости и слухи на 6 дней раньше эфиров — не вымысел фанатов телестройки, а техническая
особенность съемочного процесса и подготовки серий. Выпускать происходящее на реалити-шоу в прямой эфир
не представляется возможным, как по техническим так по этическим причинам, ведь для начала требуется вырезать
то, что показывать на телевидении нельзя, а затем собрать смонтировать то, что заинтересует телезрителя.
Иногда сами участники размещают инсайдерскую информацию на личных страницах или фан. комьюнити.

Посетители Шлока на страницах нашего сайта получают инфу о сплетнях и новостях в
формате личных мнений или сказок, что делает публикации ресурса выделяющимися в потоке сухих новостей.
Хотите получать свежие слухи и новости на 6 дней раньше выпусков — присоединяйтесь к нашему сообществуи
не пропустите последнюю информацию. Публикации авторов — рассказ о ситуациях. Авторы ни в коем случае не
навязывают читателям личное мнение, высказывая собственную точку зрения.

Новости отображены на главное странице schlock.ru, но архив событий за
годы существования проекта (с 2004 года) доступен для чтения. Добро пожаловать!