Основная функция: Основная функция — это… Что такое Основная функция? – Пространство основных функций — Википедия
Основная функция — это… Что такое Основная функция?
Обобщённая фу́нкция или распределе́ние — математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах.
Понятие обобщённой функции даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, точечного заряда, точечного диполя, (пространственную) плотность простого или двойного слоя, интенсивность мгновенного источника и т. д.
С другой стороны, в понятии обобщённой функции находит отражение тот факт, что реально нельзя измерить значение физической величины в точке, а можно измерять лишь её средние значения в малых окрестностях данной точки. Таким образом, техника обобщённых функций служит удобным и адекватным аппаратом для описания распределений различных физических величин.
Обобщённые функции были введены впервые в конце 20-х годов XX в. Дираком в его исследованиях по квантовой механике, где он систематически использует понятие δ-функции и её производных.
Основы математической теории обобщённых функций были заложены Соболевым при решении задачи Коши для гиперболических уравнений, а в 50-х годах Шварц дал систематическое изложение теории обобщённых функций и указал многие применения.
В дальнейшем теория обобщённых функций интенсивно развивалась многими математиками и физиками-теоретиками, главным образом в связи с потребностями теоретической и математической физики и теории дифференциальных уравнений [1].
Определение
Формально обобщённая функция f определяется как линейный непрерывный функционал над тем или иным векторным пространством достаточно «хороших функций» (так называемых основных функций) 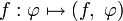 . Важным примером основного пространства является пространство
. Важным примером основного пространства является пространство 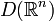
— совокупность финитных  -функций на
-функций на  , снабжённая естественной для неё топологией: последовательность функций из
, снабжённая естественной для неё топологией: последовательность функций из 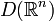 сходится, если их носители принадлежат фиксированному шару и в нём они
сходится, если их носители принадлежат фиксированному шару и в нём они 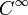 -сходятся.
-сходятся.
Сопряжённое пространство к 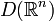 есть пространство обобщённых функций
есть пространство обобщённых функций 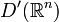 .
.
Сходимость последовательности обобщённых функций из 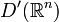 определяется как слабая сходимость функционалов из
определяется как слабая сходимость функционалов из 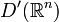 , то есть
, то есть 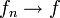 , в
, в 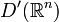 означает, что
означает, что 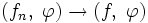 , для любой
, для любой 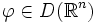 .
.
Для того, чтобы линейный функционал f на 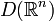 был обобщённой функцией, то есть
был обобщённой функцией, то есть 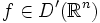 , необходимо и достаточно, чтобы для любого ограниченного открытого множества Ω существовали числа K и m такие, что
, необходимо и достаточно, чтобы для любого ограниченного открытого множества Ω существовали числа K и m такие, что
для всех 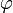 с носителем в Ω.
с носителем в Ω.
Если в неравенстве число m можно выбрать не зависящим от Ω, то обобщённая функция f имеет конечный порядок; наименьшее такое m называется порядком f.
Простейшими примерами обобщённых функций являются функционалы, порождаемые локально суммируемыми функциями
Обобщённые функции, определяемые локально суммируемыми в функциями f(x) по этой формуле, называются регулярными; остальные обобщённые функции называются сингулярными.
Обобщённые функции вообще говоря, не имеют значений в отдельных точках. Тем не менее можно говорить о совпадении обобщённой функции с локально суммируемой функцией на открытом множестве: обобщённая функция f из 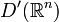 совпадает в Ω с локально суммируемой в Ω функцией f0(x), если
совпадает в Ω с локально суммируемой в Ω функцией f0(x), если
для всех 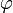 с носителм в Ω. В частности, при f0 = 0 получается определение того, что обобщённая функция f обращается в нуль внутри Ω.
с носителм в Ω. В частности, при f0 = 0 получается определение того, что обобщённая функция f обращается в нуль внутри Ω.
Множество точек, ни в какой окрестности которых обобщённая функция не обращается в ноль, называется носителем обобщённой функции f и обозначается 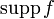 . Если
. Если 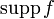 компактен, то обобщённая функция f называется финитной.
компактен, то обобщённая функция f называется финитной.
Примеры
- Любая локально конечная мера μ определяет обобщённую функцию fμ
- В частности,
- Примером сингулярной обобщённой функции в
 служит δ-функция Дирака
служит δ-функция Дирака
- Она описывает плотность массы 1, сосредоточенной в точке x = 0. δ-функция имеет порядок 1.
- Поверхностная δ-функция. Пусть S — кусочно гладкая поверхность и λ — непрерывная функция на S. Обобщённая функция
 определяется равенством
определяется равенством
- При этом
 — сингулярная обобщённая функция. Эта обобщённая функция описывает пространственную плотность масс пли зарядов, сосредоточенных на поверхности S с поверхностной плотностью λ (плотность простого слоя).
— сингулярная обобщённая функция. Эта обобщённая функция описывает пространственную плотность масс пли зарядов, сосредоточенных на поверхности S с поверхностной плотностью λ (плотность простого слоя).
- Примером сингулярной обобщённой функции в
- Обобщённая функция
 определяемая равенством
определяемая равенством
- (для гладких финитных функций этому интегралу можно придать смысл) функция ρ сингулярна и её порядок равен 2, однако на открытом множестве
 она регулярна и совпадает с
она регулярна и совпадает с  .
.
Операции
Линейные операции над обобщёнными функциями вводятся как расширение соответствующих операций над основными функциями.
Замена переменных
Пусть 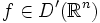 и
и 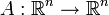 — гладкая замена переменных. Обобщённая функция
— гладкая замена переменных. Обобщённая функция 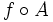 определяется равенством
определяется равенством
где J(A) обозначает якобиан A. Эту формулу можно применять в частности к линейному отображению A, она позволяет определить трансляционно инвариантные, сферически симметричные, центрально симметричные, однородные, периодические, лоренц-инвариантные и т. д. обобщённые функции.
Произведение
Чаще всего определяется произведение обобщённых функций на обычные, а произведение обобщённых функций остается неопределенным.
Пусть 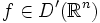 и
и 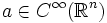 . Произведение af = fa определяется равенством
. Произведение af = fa определяется равенством
Например aδ = a(0)δ, xρ = 1. Для обычных локально суммируемых функций произведение af совпадает с обычным умножением функций f(x) и a(x).
Однако эта операция произведения вообще говоря не допускает распространения на любые обобщённые функции так, чтобы она была ассоциативной и коммутативной.
Действительно, в противном случае получилось бы противоречие:
В частности, Ю. М. Широков построил некоммутативную алгебру обобщённых функций[2][3].
Дифференцирование
Пусть 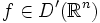 . Обобщённая (слабая) производная обобщённой функции
. Обобщённая (слабая) производная обобщённой функции 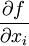 определяется равенством
определяется равенством
Так как операция 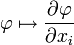 линейна и непрерывна из
линейна и непрерывна из 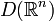 в
в 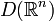 , то функционал, определяемый правой частью равенства, есть обобщённая функция.
, то функционал, определяемый правой частью равенства, есть обобщённая функция.
Свойства
- Пространство
 — полное: если последовательность обобщённых функций fi из
— полное: если последовательность обобщённых функций fi из  такова, что для любой функции
такова, что для любой функции  числовая последовательность
числовая последовательность  сходится, то функционал
сходится, то функционал
- принадлежит
 .
.
Примеры
Дельта-функция получается при вычислении интеграла Фурье от константы:
Примечания
- ↑ Обобщенные функции и действия над ними.
- ↑ Ю. М. Широков, Алгебра одномерных обобщенных функций. — Теоретическая и математическая физика. — 1979. — том 39. — № 3. — стр. 291—301.
- ↑ Г. К. Толоконников. Об Алгебрах Ю. М. Широкова. — Теоретическая и математическая физика. — 1979. — том 39. — № 3. — стр. 366—375.
См. также
Wikimedia Foundation.
2010.
Пространство основных функций — Википедия
Материал из Википедии — свободной энциклопедии
Пространство основных функций — структура, с помощью которой строится пространство обобщённых функций (пространство линейных функционалов на пространстве основных функций).
Обобщённые функции имеют большое значение в математической физике, а пространство основных функций используется как основа для строительства обобщённых функций (формально это область определения соответствующих обобщенных функций). Дифференциальные уравнения рассматриваются в т. н. слабом смысле, то есть рассматривается не поточечное равенство, а равенство соответствующих регулярных линейных функционалов на подходящем пространстве основных функций. См. пространства Соболева.
Обычно в качестве пространства основных функций D(Ω){\displaystyle {\mathcal {D}}(\Omega )} выбирается пространство бесконечно дифференцируемых функций с компактным носителем (т. н. финитных функций) C0∞(Ω){\displaystyle C_{0}^{\infty }(\Omega )}, на котором вводится следующая сходимость (а значит и топология):
Последовательность {uj}j=1∞⊂D(Ω){\displaystyle \left\{u_{j}\right\}_{j=1}^{\infty }\subset {\mathcal {D}}(\Omega )} сходится к u∈D(Ω){\displaystyle u\in {\mathcal {D}}(\Omega )}, если:
- Функции uj{\displaystyle u_{j}} равномерно финитны, то есть ∃K{\displaystyle \exists K} — компакт в Ω{\displaystyle \Omega } и в том числе ∀jsuppuj⊂K{\displaystyle \forall j\;\mathrm {supp} \,u_{j}\subset K}.
- ∀αDαuj(x)→Dαu(x){\displaystyle \forall \alpha \;D^{\alpha }u_{j}(x)\to D^{\alpha }u(x)} равномерно по x{\displaystyle x}.
Здесь Ω{\displaystyle \Omega } — ограниченная область в Rn{\displaystyle \mathbb {R} ^{n}}.
Для вопросов преобразования Фурье используются обобщённые функции медленного роста. Для них в качестве основного выбирается класс Шварца S=S(Rn){\displaystyle {\mathcal {S}}={\mathcal {S}}(\mathbb {R} ^{n})} — бесконечно гладких на Rn{\displaystyle \mathbb {R} ^{n}} функций, убывающих при |x|→∞{\displaystyle |x|\to \infty } быстрее любой степени |x|−1{\displaystyle |x|^{-1}} вместе со всеми своими производными. Сходимость на нём определяется следующим образом: последовательность функций ϕ1,ϕ2,…{\displaystyle \phi _{1},\phi _{2},\dots } сходится к ϕ∗{\displaystyle \phi ^{*}}, если
- ∀α,β∈N |x|αDβϕj(x)→|x|αDβϕ∗(x){\displaystyle \forall \alpha ,\beta \in \mathbb {N} \ |x|^{\alpha }D^{\beta }\phi _{j}(x)\to |x|^{\alpha }D^{\beta }\phi ^{*}(x)} равномерно по x{\displaystyle x}.
Выбор класса Шварца для построения преобразования Фурье на пространстве обобщенных функций обуславливается тем, что преобразование Фурье является автоморфизмом на классе Шварца.
Основная функция Википедия
Обобщённая фу́нкция или распределе́ние — математическое понятие, обобщающее классическое понятие функции.
Потребность в таком обобщении возникает во многих физических и математических задачах.
Понятие обобщённой функции даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, точечного заряда, точечного диполя, (пространственную) плотность простого или двойного слоя, интенсивность мгновенного источника и т. д.
С другой стороны, в понятии обобщённой функции находит отражение тот факт, что реально нельзя измерить значение физической величины в точке, а можно измерять лишь её средние значения в малых окрестностях данной точки.
Таким образом, техника обобщённых функций служит удобным и адекватным аппаратом для описания распределений различных физических величин. Математика начала XX века не имела нужных строгих формализмов для оперирования с новым классом зависимостей величин, открытых в физике.
Важный вклад в формирование нового математического подхода к понятию функции в физике принадлежит Η. Μ. Гюнтеру, который предлагал рассматривать вместо точечных характеристик типа плотности соответствующие функции множеств еще в 1916 году[1] и пытался переосмылить на этой основе понятие решения уравнения математической физики. Однако Н.М. Гюнтер не связывал эти идеи с нарождающимся функциональным анализом и квантовой механикой. Фундаментальные идеи, основанные на использовании пространств финитных функций и принципиально новом понятии обобщенной производной были сформулированы в 1935 году С. Л. Соболевым[2]. К аналогичным идеям самостоятельно через десять лет пришел выдающийся французский математик Л. Шварц, привлекший разработанную к тому времени теорию локально выпуклых пространств и построивший преобразование Фурье обобщенных функций[3]. Соболев и Шварц являются создателями теории распределений — обобщенных функций. Обобщённые функции эмпирически использовались Дираком в его исследованиях по квантовой механике[4][5].
В дальнейшем теория обобщённых функций интенсивно развивалась многими математиками и физиками-теоретиками, главным образом в связи с потребностями теоретической и математической физики и теории дифференциальных уравнений[6].
Определение[ | ]
Формально обобщённая функция f{\displaystyle f} определяется как линейный непрерывный функционал (f,φ){\displaystyle \left(f,\varphi \right)} над тем или иным векторным пространством достаточно «хороших функций» φ{\displaystyle \varphi } (так называемых основных функций): f:φ↦(f,φ){\displaystyle f:\varphi \mapsto (f,\;\varphi )}[7].
Условие линейности: (f,α1φ1+α2φ2)=α
Обобщённая функция — Википедия
Обобщённая фу́нкция или распределе́ние — математическое понятие, обобщающее классическое понятие функции.
Потребность в таком обобщении возникает во многих физических и математических задачах.
Понятие обобщённой функции даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, точечного заряда, точечного диполя, (пространственную) плотность простого или двойного слоя, интенсивность мгновенного источника и т. д.
С другой стороны, в понятии обобщённой функции находит отражение тот факт, что реально нельзя измерить значение физической величины в точке, а можно измерять лишь её средние значения в малых окрестностях данной точки.
Таким образом, техника обобщённых функций служит удобным и адекватным аппаратом для описания распределений различных физических величин. Математика начала XX века не имела нужных строгих формализмов для оперирования с новым классом зависимостей величин, открытых в физике.
Важный вклад в формирование нового математического подхода к понятию функции в физике принадлежит Η. Μ. Гюнтеру, который предлагал рассматривать вместо точечных характеристик типа плотности соответствующие функции множеств еще в 1916 году[1] и пытался переосмылить на этой основе понятие решения уравнения математической физики. Однако Н.М. Гюнтер не связывал эти идеи с нарождающимся функциональным анализом и квантовой механикой. Фундаментальные идеи, основанные на использовании пространств финитных функций и принципиально новом понятии обобщенной производной были сформулированы в 1935 году С. Л. Соболевым[2]. К аналогичным идеям самостоятельно через десять лет пришел выдающийся французский математик Л. Шварц, привлекший разработанную к тому времени теорию локально выпуклых пространств и построивший преобразование Фурье обобщенных функций[3]. Соболев и Шварц являются создателями теории распределений — обобщенных функций. Обобщённые функции эмпирически использовались Дираком в его исследованиях по квантовой механике
В дальнейшем теория обобщённых функций интенсивно развивалась многими математиками и физиками-теоретиками, главным образом в связи с потребностями теоретической и математической физики и теории дифференциальных уравнений[6].
Формально обобщённая функция f{\displaystyle f} определяется как линейный непрерывный функционал (f,φ){\displaystyle \left(f,\varphi \right)} над тем или иным векторным пространством достаточно «хороших функций» φ{\displaystyle \varphi } (так называемых основных функций): f:φ↦(f,φ){\displaystyle f:\varphi \mapsto (f,\;\varphi )}[7].
Условие линейности: (f,α1φ1+α2φ2)=α1(f,φ1)+α2(f,φ2){\displaystyle \left(f,\alpha _{1}\varphi _{1}+\alpha _{2}\varphi _{2}\right)=\alpha _{1}\left(f,\varphi _{1}\right)+\alpha _{2}\left(f,\varphi _{2}\right)}.
Условие непрерывности: если φν→0{\displaystyle \varphi _{\nu }\rightarrow 0}, то (f,φν)→0{\displaystyle \left(f,\varphi _{\nu }\right)\rightarrow 0}.
Важным примером основного пространства является пространство D(Rn){\displaystyle D(\mathbb {R} ^{n})} — совокупность финитных C∞{\displaystyle C^{\infty }}-функций на Rn{\displaystyle \mathbb {R} ^{n}}, снабжённая естественной для неё топологией: последовательность функций из D(Rn){\displaystyle D(\mathbb {R} ^{n})} сходится, если их носители принадлежат фиксированному шару и в нём они C∞{\displaystyle C^{\infty }}-сходятся.
Сопряжённое пространство к D(Rn){\displaystyle D(\mathbb {R} ^{n})} есть пространство обобщённых функций D′(Rn){\displaystyle D'(\mathbb {R} ^{n})}.
Сходимость последовательности обобщённых функций из D′(Rn){\displaystyle D'(\mathbb {R} ^{n})} определяется как слабая сходимость функционалов из D′(Rn){\displaystyle D'(\mathbb {R} ^{n})}, то есть fn→f{\displaystyle f_{n}\to f}, в D′(Rn){\displaystyle D'(\mathbb {R} ^{n})} означает, что (fn,φ)→(f,φ){\displaystyle (f_{n},\;\varphi )\to (f,\;\varphi )}, для любой φ∈D(Rn){\displaystyle \varphi \in D(\mathbb {R} ^{n})}.
Для того, чтобы линейный функционал f{\displaystyle f} на D(Rn){\displaystyle D(\mathbb {R} ^{n})} был обобщённой функцией, то есть f∈D′(Rn){\displaystyle f\in D'(\mathbb {R} ^{n})}, необходимо и достаточно, чтобы для любого ограниченного открытого множества Ω{\displaystyle \Omega } существовали числа K{\displaystyle K} и m{\displaystyle m} такие, что
- |(f,φ)|⩽K|φ|Cm{\displaystyle |(f,\;\varphi )|\leqslant K|\varphi |_{C^{m}}}
для всех φ{\displaystyle \varphi } с носителем в Ω{\displaystyle \Omega }.
Если в неравенстве число m{\displaystyle m} можно выбрать не зависящим от Ω{\displaystyle \Omega }, то обобщённая функция f{\displaystyle f} имеет конечный порядок; наименьшее такое m{\displaystyle m} называется порядком f{\displaystyle f}.
Простейшими примерами обобщённых функций являются функционалы, порождаемые локально суммируемыми функциями
- (f,φ)=∫Rnfφ.{\displaystyle (f,\;\varphi )=\int \limits _{\mathbb {R} ^{n}}f\varphi .}
Обобщённые функции, определяемые локально суммируемыми функциями f(x){\displaystyle f(x)} по этой формуле, называются регулярными; остальные обобщённые функции называются сингулярными.
Обобщённые функции, вообще говоря, не имеют значений в отдельных точках. Тем не менее можно говорить о совпадении обобщённой функции с локально суммируемой функцией на открытом множестве: обобщённая функция f{\displaystyle f} из D′(Rn){\displaystyle D'(\mathbb {R} ^{n})} совпадает в Ω{\displaystyle \Omega } с локально суммируемой в Ω{\displaystyle \Omega } функцией f0(x){\displaystyle f_{0}(x)}, если
- (f,φ)=(f0,φ){\displaystyle (f,\;\varphi )=(f_{0},\;\varphi )}
для всех φ{\displaystyle \varphi } с носителем в Ω{\displaystyle \Omega }. В частности, при f0=0{\displaystyle f_{0}=0} получается определение того, что обобщённая функция f{\displaystyle f} обращается в нуль внутри Ω{\displaystyle \Omega }.
Множество точек, ни в какой окрестности которых обобщённая функция не обращается в ноль, называется носителем обобщённой функции f{\displaystyle f} и обозначается suppf{\displaystyle \mathrm {supp} \,f}. Если suppf{\displaystyle \mathrm {supp} \,f} компактен, то обобщённая функция f{\displaystyle f} называется финитной.
- Любая локально конечная мера μ{\displaystyle \mu } определяет обобщённую функцию fμ{\displaystyle f_{\mu }}
- (fμ,φ)=∫φ(x)dμ(x).{\displaystyle (f_{\mu },\;\varphi )=\int \varphi (x)\,d\mu (x).}
- В частности,
- (δ,φ)=φ(0).{\displaystyle (\delta ,\;\varphi )=\varphi (0).}
- Она описывает плотность массы 1, сосредоточенной в точке x=0{\displaystyle x=0}. δ{\displaystyle \delta }-функция имеет порядок 1.
- (fS,λ,φ)=∫Sφλ.{\displaystyle (f_{S,\;\lambda },\;\varphi )=\int \limits _{S}\varphi \lambda .}
- При этом fS,λ{\displaystyle f_{S,\;\lambda }} — сингулярная обобщённая функция. Эта обобщённая функция описывает пространственную плотность масс или зарядов, сосредоточенных на поверхности S{\displaystyle S} с поверхностной плотностью λ{\displaystyle \lambda } (плотность простого слоя).
- Обобщённая функция ρ∈D′(R){\displaystyle \rho \in D'(\mathbb {R} )} определяемая равенством
- (ρ,φ)=v.p.∫Rφ(x)xdx{\displaystyle (\rho ,\;\varphi )=\operatorname {v.\!p.} \int \limits _{\mathbb {R} }{\frac {\varphi (x)}{x}}\,dx}
- (для гладких финитных функций этому интегралу можно придать смысл) функция ρ{\displaystyle \rho } сингулярна и её порядок равен 2, однако на открытом множестве R∖{0}{\displaystyle \mathbb {R} \backslash \{0\}} она регулярна и совпадает с 1x{\displaystyle {\frac {1}{x}}}.
Линейные операции над обобщёнными функциями вводятся как расширение соответствующих операций над основными функциями.
Замена переменных[править | править код]
Пусть f∈D′(Rn){\displaystyle f\in D'(\mathbb {R} ^{n})} и A:Rn→Rn{\displaystyle A:\mathbb {R} ^{n}\to \mathbb {R} ^{n}} — гладкая замена переменных. Обобщённая функция f∘A{\displaystyle f\circ A} определяется равенством
- (f∘A,φ)=(f,φ∘A−1J(A)),{\displaystyle (f\circ A,\;\varphi )=(f,\;\varphi \circ A^{-1}J(A)),}
где J(A){\displaystyle J(A)} обозначает якобиан A{\displaystyle A}. Эту формулу можно применять в частности к линейному отображению A{\displaystyle A}, она позволяет определить трансляционно инвариантные, сферически симметричные, центрально симметричные, однородные, периодические, лоренц-инвариантные и т. д. обобщённые функции.
Произведение[править | править код]
Чаще всего определяется произведение обобщённых функций на обычные, а произведение обобщённых функций остается неопределенным.
Пусть f∈D′(Rn){\displaystyle f\in D'(\mathbb {R} ^{n})} и a∈C∞(Rn){\displaystyle a\in C^{\infty }(\mathbb {R} ^{n})}. Произведение af{\displaystyle af} определяется равенством
- (af,φ)=(f,aφ).{\displaystyle (af,\;\varphi )=(f,\;a\varphi ).}
Например aδ=a(0)δ{\displaystyle a\delta =a(0)\delta }, xρ=1{\displaystyle x\rho =1}. Для обычных локально суммируемых функций произведение af{\displaystyle af} совпадает с обычным умножением функций f(x){\displaystyle f(x)} и a(x){\displaystyle a(x)}.
Однако эта операция произведения, вообще говоря, не допускает распространения на любые обобщённые функции так, чтобы она была ассоциативной и коммутативной.
Действительно, в противном случае получилось бы противоречие:
- (xδ)ρ=0⋅ρ=0,{\displaystyle (x\delta )\rho =0\cdot \rho =0,}
- (xρ)δ=1⋅δ=δ.{\displaystyle (x\rho )\delta =1\cdot \delta =\delta .}
Впрочем, возможно определить умножение любых обобщённых функций, если снять достаточно жёсткое требование, чтобы сужение этой операции на множество непрерывных функций совпадало с обычным произведением. В частности, Ю. М. Широков построил некоммутативную алгебру обобщённых функций[8][9]. Нынче в Западной Европе и Америке очень популярной (см., напр., список цитированных работ в[10]) является теория обобщённых функций Коломбо (одним из первоисточников которой является книга[11], для первоначального ознакомления с гораздо чаще используемой на практике т. н. «специальной» алгеброй Коломбо можно просмотреть параграф 8.5 из[12]). В рамках этой теории обобщённые функции являются классами эквивалентности некоторой факторалгебры. Преимуществом алгебры Коломбо является то, что она как ассоциативна, так и коммутативна. Умножение обобщённых функций Коломбо совпадает с обычным умножением при сужении на множество всех гладких (то есть, бесконечно непрерывно дифференцируемых) функций, несостыковка же с умножением непрерывных (но не гладких) функций разрешается при помощи введения понятия ассоциации (менее строгого, чем понятие эквивалентности). Также рассматриваемое умножение прекрасно согласуется со стандартными операциями классического анализа (напр., дифференцированием).
Дифференцирование[править | править код]
Пусть f∈D′(Rn){\displaystyle f\in D'(\mathbb {R} ^{n})}. Обобщённая (слабая) производная обобщённой функции ∂f∂xi{\displaystyle {\frac {\partial f}{\partial x_{i}}}} определяется равенством
- (∂f∂xi,φ)=−(f,∂φ∂xi).{\displaystyle \left({\frac {\partial f}{\partial x_{i}}},\;\varphi \right)=-\left(f,\;{\frac {\partial \varphi }{\partial x_{i}}}\right).}
Так как операция φ↦∂φ∂xi{\displaystyle \varphi \mapsto {\frac {\partial \varphi }{\partial x_{i}}}} линейна и непрерывна из D(Rn){\displaystyle D(\mathbb {R} ^{n})} в D(Rn){\displaystyle D(\mathbb {R} ^{n})}, то функционал, определяемый правой частью равенства, есть обобщённая функция.
- (f,φ)=lim
Функция (математика) — Википедия
У этого термина существуют и другие значения, см. функция.
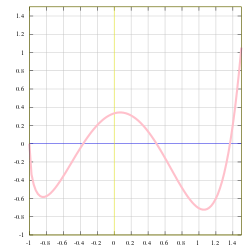 График функции
График функции
f(x)=(4×3−6×2+1)x+13−x{\displaystyle {\begin{aligned}&\scriptstyle \\&\textstyle f(x)={\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}.
Фу́нкция (отображе́ние, опера́тор, преобразова́ние) — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так, значение переменной x{\displaystyle x} однозначно определяет значение выражения x2{\displaystyle x^{2}},
также значение месяца однозначно определяет значение следующего за ним месяца.
Другой пример функции: каждому человеку можно однозначно поставить в соответствие его биологическую мать.
Аналогично, задуманный заранее алгоритм по значению входного данного выдаёт значение выходного данного.
Часто под термином «функция» понимается числовая функция, то есть функция, которая ставит одни числа в соответствие другим. Эти функции удобно представлять в виде графиков.
Термин «функция» (в некотором более узком смысле) был впервые использован Лейбницем (1692 год). В свою очередь, Иоганн Бернулли в письме к тому же Лейбницу употребил этот термин в смысле, более близком к современному[1][2].
Первоначально понятие функции было неотличимо от понятия аналитического представления. Впоследствии появилось определение функции, данное Эйлером (1751 год), затем — у Лакруа (1806 год), — уже практически в современном виде. Наконец, общее определение функции (в современной форме, но для числовых функций) было дано Лобачевским (1834 год) и Дирихле (1837 год)[3].
К концу XIX века понятие функции переросло рамки числовых систем. Сначала понятие функции было распространено на векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение[2].
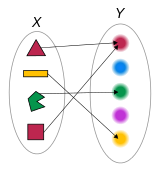 Функция, сопоставляющая каждой из четырёх фигур её цвет.
Функция, сопоставляющая каждой из четырёх фигур её цвет.
Наиболее строгим является теоретико-множественное определение функции (на основе понятия бинарного отношения). Часто вместо определения функции даётся понятие функции, то есть описание математического объекта с помощью понятий обычного языка, таких как «закон», «правило» или «соответствие».
Понятие функции[править | править код]
Говорят, что на множестве X{\displaystyle X} имеется функция (отображение, операция, оператор) f{\displaystyle f} со значениями из множества Y{\displaystyle Y}, если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} по правилу f{\displaystyle f} поставлен в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}[1].
Говорят также, что функция f{\displaystyle f} отображает множество X{\displaystyle X} в множество Y{\displaystyle Y}. Функцию обозначают также записью y=f(x){\displaystyle y=f(x)}.
Если используется термин оператор, то говорят, что оператор f{\displaystyle f} действует из множества X{\displaystyle X} в множество Y{\displaystyle Y} и добавляют запись y=fx{\displaystyle y=fx}.
Если хотят подчеркнуть, что правило соответствия считается известным, то говорят, что на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из Y{\displaystyle Y}. Если функция f{\displaystyle f} должна находиться в результате решения какого-нибудь уравнения, то говорят, что f{\displaystyle f} — неизвестная или неявно заданная функция. Но в любом случае, функция, по смыслу этого понятия, считается заданной, хотя и косвенно.
Заметим, что в формулировке понятия функции требование соответствия «по правилу» является повтором, поскольку оно содержится в понятии однозначного соответствия. Формулировка понятия функции без понятия правило и необходимости его обозначать:
Говорят, что на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из Y{\displaystyle Y}, если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} поставлен в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}[4].
Например, функция, заданная на X{\displaystyle X} таблицей пар элементов x{\displaystyle x} и y{\displaystyle y}, содержит и правило соответствия для каждого элемента из X{\displaystyle X}, поскольку значения функции при переходе от элемента к элементу множества X{\displaystyle X} располагаются по вполне определенному правилу.
Для числовых функций, часто задаваемых формулами, понятие функции формулируется как соответствие между элементами множеств посредством правила. Правило не обозначается, чтобы избежать совпадения обозначений правила и функции:
Если каждому элементу x{\displaystyle x} из множества X{\displaystyle X} по какому-либо правилу ставится в соответствие некоторый элемент y{\displaystyle y} из множества Y{\displaystyle Y}, то указанное соответствие называется функцией y=f(x){\displaystyle y=f(x)}, заданной на множестве X{\displaystyle X} со значениями из Y{\displaystyle Y}[3][5].
Буква f{\displaystyle f} в этом обозначении — индивидуальный знак функции.
Итак, функция y=f(x){\displaystyle y=f(x)} (или кратко: функция f(x){\displaystyle f(x)} или f{\displaystyle f}) представляет собой тройку объектов: X,f,Y{\displaystyle X,f,Y}, где
Обозначенный буквой x{\displaystyle x} каждый элемент множества X{\displaystyle X} называется независимой переменной или аргументом функции. Множество X{\displaystyle X} при этом называется областью изменения переменной x{\displaystyle x}.
Элемент y{\displaystyle y}, соответствующий фиксированному элементу x{\displaystyle x} называется частным значением функции в точке x{\displaystyle x}.
Совокупность всех частных значений y{\displaystyle y}, обозначаемая символом {y}{\displaystyle \{y\}}, называется множеством значений функции.
Теоретико-множественное определение[править | править код]
Понятие множества упорядоченных пар (отношения) позволяет исключить из формулировки понятия функции не только понятие правило, но и понятие соответствие, к которому сводится понятие функции в обычных формулировках предыдущего подраздела.
Таким образом, для функции можно сформулировать определение, использующее только начальные математические понятия:
- Функцией f{\displaystyle f} называется множество упорядоченных пар (x,y)∈X×Y{\displaystyle (x,y)\in X\times Y}, таких, что пары существуют для всех элементов множества X{\displaystyle X}, и, если первые элементы пар совпадают, то совпадают и вторые их элементы[1].
При этом:
Функции f{\displaystyle f} и g{\displaystyle g} называются равными, если их графики совпадают[6].
Поскольку равенство функций (в любой формулировке понятия функции) включает в себя не только совпадение правил соответствия между элементами множеств, но и совпадение областей задания, то функции f1(x)=x:R→R{\displaystyle f_{1}(x)=x:\mathbb {R} \to \mathbb {R} } и f2(x)=x:R+→R{\displaystyle f_{2}(x)=x:\mathbb {R} ^{+}\to \mathbb {R} }, где R{\displaystyle \mathbb {R} } — множество вещественных чисел, а R+{\displaystyle \mathbb {R} ^{+}} — множество положительных вещественных чисел, являются разными функциями.
Более общим, включающим в себя не только однозначные функции, является следующее определение функции:
Функцией f{\displaystyle f} называется любое множество упорядоченных пар (x,y)∈X×Y{\displaystyle (x,y)\in X\times Y}[1][нет в источнике].
При этом:
- Множество X{\displaystyle X} называется областью отправления функции. Множество всех элементов x∈X{\displaystyle x\in X}, для которых существует пара (x,y)∈f{\displaystyle (x,y)\in f}, называется областью задания функции;
- множество Y{\displaystyle Y} называется областью прибытия функции. Множество всех элементов y∈Y{\displaystyle y\in Y}, для которых существует пара (x,y)∈f{\displaystyle (x,y)\in f}, называется множеством значений функции.
Если на множестве X{\displaystyle X} задана функция f{\displaystyle f}, принимающая значения из множества Y{\displaystyle Y}, то
- этот факт записывают в виде f:X→Y{\displaystyle f\colon X\to Y} или X⟶fY{\displaystyle X{\stackrel {f}{\longrightarrow }}Y};
- множество X{\displaystyle X} — область задания функции f{\displaystyle f} — обозначается символом D(f){\displaystyle D(f)} или domf;{\displaystyle \mathrm {dom} \,f;}
- множество Y{\displaystyle Y} — область значений[3] функции f{\displaystyle f};
- множество значений {y}{\displaystyle \{y\}} функции f{\displaystyle f} обозначается символом E(f){\displaystyle E(f)} или codf{\displaystyle \mathrm {cod} \,f} (ranf{\displaystyle \mathrm {ran} \,f}).
- Если область значений Y{\displaystyle Y} и множество значений E(f){\displaystyle E(f)} совпадают, то говорят, что f{\displaystyle f} отображает множество X{\displaystyle X} на Y{\displaystyle Y}.
- Функция, заданная на множестве X{\displaystyle X}, наиболее часто обозначается как соответствие между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}:
- y=f(x){\displaystyle y=f(x)}, или кратко:f(x){\displaystyle f(x)} или f{\displaystyle f};
- x↦y{\textstyle x\mapsto y} или x↦f(x){\displaystyle x\mapsto f(x)};
- для сокращения числа обозначений знак функции, заданной на множестве X{\displaystyle X}, может обозначаться той же буквой, что и каждое значение функции:
- y=y(x){\displaystyle y=y(x)}, z=z(x){\displaystyle z=z(x)};
- функция обозначается и как функция f{\displaystyle f}, которая отображает множество X{\displaystyle X} в Y{\displaystyle Y}с обозначением соответствия между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y}:
- f:x↦y{\displaystyle f\colon x\mapsto y} или f:y=f(x){\displaystyle f\colon y=f(x)};
- реже используется обозначение функции как соответствие между элементами x∈X{\displaystyle x\in X} и y∈Y{\displaystyle y\in Y} без скобок: y=fx{\displaystyle y=fx}, y=f∘x{\displaystyle y=f\circ x} или y=xf{\displaystyle y=xf},
- а там, где необходимо подчеркнуть двойственность, используются обозначения со скобками: y=(f,x){\displaystyle y=(f,x)} или y=(x,f){\displaystyle y=(x,f)};
- также существует и операторное обозначение y=xf{\displaystyle y=x^{f}}, которое можно встретить в общей алгебре.
- В лямбда-исчислении Чёрча используется обозначение λx.y{\displaystyle \lambda x.y} .
Функции нескольких аргументов[править | править код]
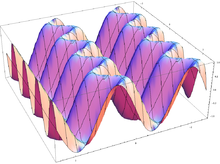 График функции двух переменных f(x,y)=sin(x−sin(2y)){\displaystyle f(x,y)=\sin(x-\sin(2y))}
График функции двух переменных f(x,y)=sin(x−sin(2y)){\displaystyle f(x,y)=\sin(x-\sin(2y))}
Понятие функции легко обобщается на случай функции многих аргументов.
Если множество X{\displaystyle X} представляет собой декартово произведение множеств X1,X2,…,Xn{\
Основная функция 🎓²
Обобщённая фу́нкция или распределе́ние — математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах
.
Понятие обобщённой функции даёт возможность выразить в математически корректной форме такие идеализированные понятия, как плотность материальной точки, точечного заряда, точечного диполя, (пространственную) плотность простого или двойного слоя, интенсивность мгновенного источника и т. д
.
С другой стороны, в понятии обобщённой функции находит отражение тот факт, что реально нельзя измерить значение физической величины в точке, а можно измерять лишь её средние значения в малых окрестностях данной точки. Таким образом, техника обобщённых функций служит удобным и адекватным аппаратом для описания распределений различных физических величин
.
Обобщённые функции были введены впервые в конце 20-х годов XX в. Дираком в его исследованиях по квантовой механике, где он систематически использует понятие δ-функции и её производных
.
Основы математической теории обобщённых функций были заложены Соболевым при решении задачи Коши для гиперболических уравнений, а в 50-х годах Шварц дал систематическое изложение теории обобщённых функций и указал многие применения
.
В дальнейшем теория обобщённых функций интенсивно развивалась многими математиками и физиками-теоретиками, главным образом в связи с потребностями теоретической и математической физики и теории дифференциальных уравнений [1]
.
Формально обобщённая функция f определяется как линейный непрерывный функционал над тем или иным векторным пространством достаточно «хороших функций» (так называемых основных функций)  . Важным примером основного пространства является пространство
. Важным примером основного пространства является пространство  — совокупность финитных
— совокупность финитных  -функций на
-функций на  , снабжённая естественной для неё топологией: последовательность функций из
, снабжённая естественной для неё топологией: последовательность функций из  сходится, если их носители принадлежат фиксированному шару и в нём они
сходится, если их носители принадлежат фиксированному шару и в нём они  -сходятся
-сходятся
.
Сопряжённое пространство к  есть пространство обобщённых функций
есть пространство обобщённых функций 
.
Сходимость последовательности обобщённых функций из  определяется как слабая сходимость функционалов из
определяется как слабая сходимость функционалов из  , то есть
, то есть  , в
, в  означает, что
означает, что  , для любой
, для любой 
.
Для того, чтобы линейный функционал f на  был обобщённой функцией, то есть
был обобщённой функцией, то есть  , необходимо и достаточно, чтобы для любого ограниченного открытого множества Ω существовали числа K и m такие, что
, необходимо и достаточно, чтобы для любого ограниченного открытого множества Ω существовали числа K и m такие, что
для всех  с носителем в Ω
с носителем в Ω
.
Если в неравенстве число m можно выбрать не зависящим от Ω, то обобщённая функция f имеет конечный порядок; наименьшее такое m называется порядком f
.
Простейшими примерами обобщённых функций являются функционалы, порождаемые локально суммируемыми функциями
Обобщённые функции, определяемые локально суммируемыми в функциями f(x) по этой формуле, называются регулярными; остальные обобщённые функции называются сингулярными
.
Обобщённые функции вообще говоря, не имеют значений в отдельных точках. Тем не менее можно говорить о совпадении обобщённой функции с локально суммируемой функцией на открытом множестве: обобщённая функция f из  совпадает в Ω с локально суммируемой в Ω функцией f0(x), если
совпадает в Ω с локально суммируемой в Ω функцией f0(x), если
для всех  с носителм в Ω. В частности, при f0 = 0 получается определение того, что обобщённая функция f обращается в нуль внутри Ω
с носителм в Ω. В частности, при f0 = 0 получается определение того, что обобщённая функция f обращается в нуль внутри Ω
.
Множество точек, ни в какой окрестности которых обобщённая функция не обращается в ноль, называется носителем обобщённой функции f и обозначается  . Если
. Если  компактен, то обобщённая функция f называется финитной
компактен, то обобщённая функция f называется финитной
.
- Любая локально конечная мера μ определяет обобщённую функцию fμ
- В частности,
- Примером сингулярной обобщённой функции в
 служит δ-функция Дирака
служит δ-функция Дирака
- Она описывает плотность массы 1, сосредоточенной в точке x = 0. δ-функция имеет порядок 1.
- Поверхностная δ-функция. Пусть S — кусочно гладкая поверхность и λ — непрерывная функция на S. Обобщённая функция
 определяется равенством
определяется равенством
- При этом
 — сингулярная обобщённая функция. Эта обобщённая функция описывает пространственную плотность масс пли зарядов, сосредоточенных на поверхности S с поверхностной плотностью λ (плотность простого слоя).
— сингулярная обобщённая функция. Эта обобщённая функция описывает пространственную плотность масс пли зарядов, сосредоточенных на поверхности S с поверхностной плотностью λ (плотность простого слоя).
- Примером сингулярной обобщённой функции в
- Обобщённая функция
 определяемая равенством
определяемая равенством
- (для гладких финитных функций этому интегралу можно придать смысл) функция ρ сингулярна и её порядок равен 2, однако на открытом множестве
 она регулярна и совпадает с
она регулярна и совпадает с  .
.
Линейные операции над обобщёнными функциями вводятся как расширение соответствующих операций над основными функциями
.
Замена переменных
Пусть  и
и  — гладкая замена переменных. Обобщённая функция
— гладкая замена переменных. Обобщённая функция  определяется равенством
определяется равенством
где J(A) обозначает якобиан A. Эту формулу можно применять в частности к линейному отображению A, она позволяет определить трансляционно инвариантные, сферически симметричные, центрально симметричные, однородные, периодические, лоренц-инвариантные и т. д. обобщённые функции
.
Произведение
Чаще всего определяется произведение обобщённых функций на обычные, а произведение обобщённых функций остается неопределенным
.
Пусть  и
и  . Произведение af = fa определяется равенством
. Произведение af = fa определяется равенством
Например aδ = a(0)δ, xρ = 1. Для обычных локально суммируемых функций произведение af совпадает с обычным умножением функций f(x) и a(x
).
Однако эта операция произведения вообще говоря не допускает распространения на любые обобщённые функции так, чтобы она была ассоциативной и коммутативной
.
Действительно, в противном случае получилось бы противоречие
:
В частности, Ю. М. Широков построил некоммутативную алгебру обобщённых функций[2][3]
.
Дифференцирование
Пусть  . Обобщённая (слабая) производная обобщённой функции
. Обобщённая (слабая) производная обобщённой функции  определяется равенством
определяется равенством
Так как операция  линейна и непрерывна из
линейна и непрерывна из  в
в  , то функционал, определяемый правой частью равенства, есть обобщённая функция
, то функционал, определяемый правой частью равенства, есть обобщённая функция
.
- Пространство
 — полное: если последовательность обобщённых функций fi из
— полное: если последовательность обобщённых функций fi из  такова, что для любой функции
такова, что для любой функции  числовая последовательность
числовая последовательность  сходится, то функционал
сходится, то функционал
- принадлежит
 .
.
Дельта-функция получается при вычислении интеграла Фурье от константы
:
Wikimedia Foundation.
2010.
Пространство основных функций — это… Что такое Пространство основных функций?
Пространство обобщенных функций — Обобщённая функция или распределение математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие обобщённой функции даёт возможность выразить в… … Википедия
Пространство Соболева — (в математике) функциональное пространство, состоящее из функций из пространства Лебега ( ), имеющих обобщенные производные заданного порядка из . При пространства Соболева являются банаховыми пространствами, а при p=2 пространства Соболева … Википедия
Пространство Шварца — Пространство Шварца пространство быстро убывающих функций. Формально говоря, состоит из таких бесконечно дифференцируемых вещественных функций , что при . Это значит что сама функция, и все её производные на бесконечности стремятся к нулю… … Википедия
Пространство обобщённых функций — Обобщённая функция или распределение математическое понятие, обобщающее классическое понятие функции. Потребность в таком обобщении возникает во многих физических и математических задачах. Понятие обобщённой функции даёт возможность выразить в… … Википедия
Пространство состояний (теория управления) — Пространство состояний в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение ее состояний. Содержание 1 Определение 1.1 Линейные непрерывные… … Википедия
Пространство состояний — Пространство состояний в теории управления один из основных методов описания поведения динамической системы. Движение системы в пространстве состояний отражает изменение его состояний. Содержание 1 Определение 1.1 Линейные непрерывные системы … Википедия
ФУНКЦИЙ ТЕОРИЯ — раздел математики, занимающийся изучением свойств различных функций. Теория функций распадается на две области: теорию функций действительного переменного и теорию функций комплексного переменного, различие между которыми настолько велико, что… … Энциклопедия Кольера
ОБОБЩЕННЫХ ФУНКЦИЙ ПРОСТРАНСТВО — пространство, сопряженное к пространству основных (достаточно хороших) функций. Важную роль здесь играют Фреше пространства (типа FS )и сильно сопряженные к ним (типа DFS). Пространство типа FS есть проективный предел компактной… … Математическая энциклопедия
БАНАХОВО ПРОСТРАНСТВО — В пространство, полное нормированное векторное пространство. Исходными для создания теории Б. п. послужили введенные (в 1904 18) Д. Гильбертом (D. Hilbert), М. Фреше (М. Frechet) и Ф. Рисом (F. Riesz) функциональные пространства. Именно в этих… … Математическая энциклопедия
КОНСТРУКТИВНОЕ МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — концепция метрич. пространства, используемая в конструктивной математике. Близкий смысл имеет также понятие рекурсивного метрического пространства. Список где некоторое множество конструктивных объектов (обычно слов в том или ином алфавите), р… … Математическая энциклопедия

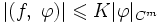
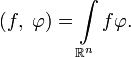
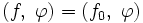
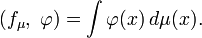
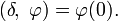
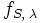 определяется равенством
определяется равенством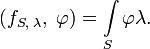
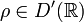 определяемая равенством
определяемая равенством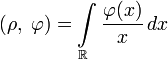
 она регулярна и совпадает с
она регулярна и совпадает с  .
.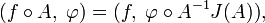
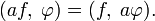
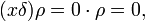
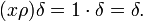
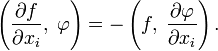
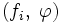 сходится, то функционал
сходится, то функционал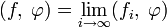
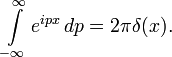





 определяется равенством
определяется равенством
 определяемая равенством
определяемая равенством
 она регулярна и совпадает с
она регулярна и совпадает с  .
.




 сходится, то функционал
сходится, то функционал
