А b c 2: Square of a Trinomial | (a + b + c)^2 Formula – Attention Required! | Cloudflare

Формулы сокращённого умножения | Алгебра

При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.

Формулы сокращённого умножения – это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.

a² + b² = (a + b)² — 2ab  –  сумма квадратов

a² — b² = (a + b)(a — b)  –  разность квадратов

(a + b)² = a² + 2ab + b²  –  квадрат суммы

(a — b)² = a² — 2ab + b²  –  квадрат разности

a³

+ b³ = (a + b)(a² — ab + b²)  –  сумма кубов

a³ — b³ = (a — b)(a² + ab + b²)  –  разность кубов

(a + b)³ = a³ + 3a²b + 3ab² + b³  –  куб суммы

(a — b)³ = a³ — 3a²b + 3ab² — b³  –  куб разности

Обратите внимание, что a и b в формулах сокращённого умножения могут быть как числами, так и выражениями.

Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения:

• Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:

  a² + b² = (a + b)² — 2ab

  Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:

  (a + b)² — 2ab = (a + b)(a + b) — 2ab =

  
  

  = a² + ab + ab + b² — 2ab = a² + b²

• Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:

  a² — b² = (a + b)(a — b)

  Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

  
  

  (a + b)(a — b) = a² — ab + ab — b² = a² — b²

• Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:

  (a + b)² = a² + 2ab + b²

  Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

  (a + b)² = (a + b)(a + b) = a² + ab + ab + b² = a² + 2ab + b²

• Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:

  (a — b)² = a² — 2ab + b²

  Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

  (a — b)² = (a — b)(a — b) = a² — ab — ab + b² = a² — 2ab + b²

• Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:

  a³ + b³ = (a + b)(a² — ab + b²)

  Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

  
  

  (a + b)(a² — ab + b²) = a³ — a²b + ab² + a²b — ab² + b³ = a³ + b³

• Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:

  a³ — b³ = (a — b)(a² + ab + b²)

  Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:

  (a — b)(a² + ab + b²) = a³ + a

  2b + ab² — a²b — ab² — b³ = a³ — b³

• Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:

  (a + b)³ = a³ + 3a²b + 3ab² + b³

  Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

  (a + b)³ = (a + b)(a + b)² = (a + b)(a² + 2ab + b²) =

  
  

  = a³ + 2

  
  
  
  
  a²b + ab² + a²b + 2ab² + b³ = a³ + 3a²b + 3ab² + b³

• Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:

  (a — b)³ = a³ — 3a²b + 3ab² — b³

  Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:

  (a — b)³ = (a — b)(a — b)² = (a — b)(a² — 2ab + b

  2) =

  
  

  = a³ — 2a²b + ab² — a²b + 2ab² — b³ = a³ — 3a²b + 3ab² — b³

Неполный квадрат суммы

Выражение:

a² + 2ab + b²

это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:

a² + ab + b²,

которое называется неполным квадратом суммы. Неполный квадрат суммы – это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.

Неполный квадрат разности

Выражение:

a² — 2ab + b²

Это квадрат разности, который также называется полным квадратом разности относительно выражения:

a² — ab + b²,

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

Формулы сокращенного умножения: таблица, примеры использования

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Формулы сокращенного умножения. Таблица

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

Формулы сокращенного умножения

1. формула квадрата суммы: a+b2=a2+2ab+b2
2. формула квадрата разности: a-b2=a2-2ab+b2
3. формула куба суммы: a+b3=a3+3a2b+3ab2+b3
4. формула куба разности: a-b3=a3-3a2b+3ab2-b3
5. формула разности квадратов: a2-b2=a-ba+b
6. формула суммы кубов: a3+b3=a+ba2-ab+b2
7. формула разности кубов: a3-b3=a-ba2+ab+b2

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы. 

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращ

Формулы сокращенного умножения

Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения. Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).

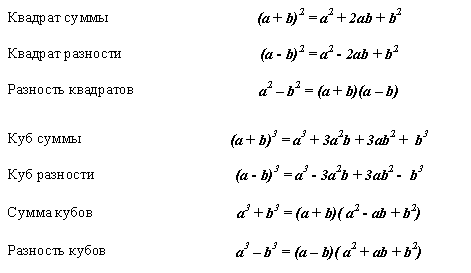
Первая формула сокращенного умножения называется разность квадратов. Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.

а² — b² = (а — b)(a + b)

Разберем для наглядности:

22² — 4² = (22-4)(22+4)=18 * 26 = 468
9а² — 4b²c² = (3a — 2bc)(3a + 2bc)

Вторая формула о сумме квадратов. Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.

(а + b)² = a² +2ab + b²

Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.

Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
112² = (100+12)²
3) Применяя формулу, получаем:

112² = (100+12)² = 100² + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544

Третья формула это квадрат разности. Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.

(а +b)² = а² — 2аb + b²

где (а — b)² равняется (b — а)². В доказательство чему, (а-b)² = а²-2аb+b² = b²-2аb + а² = (b-а)²

Четвертая формула сокращенного умножения называется куб суммы. Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.

(а+b)³ = а³ + 3а²b + 3аb² + b³

Пятая, как вы уже поняли называется куб разности. Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.

(а-b)³ = а³ — 3а²b + 3аb² — b³

Шестая называется — сумма кубов. Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.

а³ + b³ = (а+b)(а²-аb+b²)

По другому можно сказать сумму кубов можно назвать произведение в двух скобках.

Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.

а³ — b³ = (а-b)(а²+аb+b²)

И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.

Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!

Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм. Там все очень подробно написано и показано. Будет интересно!

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Формулы сокращенного умножения / Блог :: Бингоскул

Содержание:

• Таблица формул сокращенного умножения
• Примеры использования
• Формулы для квадратов
• Формулы для кубов
• Формулы для четвертой степени

Таблица формул сокращенного умножения

Примеры использования формул

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a+b)² = a²+2ab+b²

Пример: (x + 3y)² = x² + 2 ·x·3y + (3y)² = x² + 6xy + 9y²

---

 

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

(a-b)² = a²-2ab+b²

Пример: (4x –y)² = (4x)²-2·4x·y + y² = 16x² — 8xy + y²

---

Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.

a²–b² = (a–b)(a+b)

Пример: 9x² – 16y² = (3x)² – (4y)² = (3x – 4y)(3x + 4y)

---

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

(a+b)³ = a³+3a²b+3ab²+b³

Пример: (x + 2y)³ = x³ + 3·x²·2y + 3·x·(2y)² + (2n)³ = x³ + 6x²y + 12xy² + 8y³

---

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a-b)³ = a³— 3a²b+3ab²-b³

Пример: (2x – y)³ = (2x)³-3·(2x)²·y + 3·2x·y² – y³ = 8x³ – 12x²y + 6xy² – y³

---

Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.

a³+b³ = (a+b)(a²–ab+b²)

Пример: 125 + 8y³ = 5³ + (2y)³ = (5 + 2y)(5² — 5·2y + (2y)²) = (5 + 2y)(25 – 10y + 4y²)

---

Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.

a³— b³ = (a-b)(a²+ab+b²)

Пример: 64x³ – 8 = (4x)³ – 2³ = (4x – 2)((4x)² + 4x·2 + 2²) = (4x – 2)(16x² + 8x + 4)

---

Формулы для квадратов

• (a \pm b)^2= a^2 \pm 2ab + b^2
• a^2 — b^2 = (a + b)(a — b)
• (a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc

 

Формулы для кубов

• (a \pm b)^3= a^3 \pm 3a^2b +3ab^2 \pm b^3
• a^3 — b^3 = (a \pm b)(a^2\mp ab+b^2)
• (a+b+c)^3=a^3+b^3+c^3+3a^2b+3a^2c+3ab^2+3ac^2+3b^2c+3bc^2+6abc

Формулы для четвертой степени

• (a \pm b)^4= a^4 \pm 4a^3b +6a^2b^2\pm 4ab^3+b^4
• a^4 — b^4 = (a-b)(a+b)(a^2 +b^2) (выводится из a^2 — b^2)

 

---

В заданиях ЕГЭ по математике применяются формулы сокращенного умножения.

Решай с ответами задание 5 по математике база ЕГЭ

Смотри также: Основные формулы по математике