Коэффициент аннуитета: Аннуитет — Википедия – Аннуитет. Формула аннуитетного платежа. Расчет платежей — Миллион шаг за шагом
что это? Его формула расчета по кредиту
Что такое аннуитетные платежи?
Смысл аннуитетного платежа в том, что каждый месяц заемщик выплачивает банку одинаковую сумму.
Выплаты являются равными на протяжении всего периода действия договорных отношений и вносятся через равные промежутки времени (чаще всего ежемесячно).
Соответственно аннуитетный платеж – это регулярный, фиксированный взнос, включающий оплату основного кредита и процентов.
Сумма такого платежа постоянна, но пропорции процентов и «тела» в течение периода кредитования меняются. Вначале заемщик выплачивает по большей части проценты, а в конце периода – основной долг.
На сегодняшний день эта схема является наиболее распространенной, так как выгодна как для банков, так и для клиентов. Первые по итогу получают большее вознаграждение, а последний – возможность взять большую сумму займа при меньшем бюджете.
Плюсы такой системы:

- Ясность в вопросе суммы ежемесячных выплат, так как они устанавливаются в начале кредитных отношений и остаются одинаковыми до их окончания.
- Возможность получить более крупный налоговый вычет. В случае с ипотечным кредитом это может стать весьма существенным критерием. В соответствии со ст. 220 налогового кодекса РФ по такому кредиту проценты возвращаются по мере их уплаты банку каждый год. В первые годы это очень уместно, учитывая, что сумма процентных выплат будет значительно превышать сумму выплат по телу кредита. Для получения такого налогового вычета необходимо подать документы в налоговую инспекцию в соответствии с законодательством.
- Приемлемые условия и низкие критерии для получения больших сумм кредита. Аннуитетные платежи равномерно распределяются небольшими суммами и идеально подходят людям с ограниченным доходом. Именно по этой причине такая система чаще всего применяется для ипотечного и образовательного кредитования.
В качестве недостатков можно отметить следующие моменты:
- Сравнительно высокая сумма переплаты за счет процентов.
- Неравномерность пропорций выплат процентов и тела займа. Это может стать проблемой при досрочном погашении кредита, так фактически основная сумма займа начинает выплачиваться только с середины кредитного периода. Это приводит к тому, что если заемщик решит в первые годы досрочно погасить кредит ему придется вносить практически всю взятую в кредит сумму целиком, так как вносимые до этого суммы уходили на погашение процентов.


Аннуитет
Аннуитет – это широкий общий термин описывающий график погашения кредита.
Под ним могут подразумеваться следующие финансовые элементы:
- Вид срочного займа, при котором с условленной периодичностью выплачивается равная сумма, включающая как тело, так и проценты этого займа.
- Сами денежные выплаты равные друг другу и выплачиваемые через равные установленные договором промежутки времени в счет кредита.
- Договор со страховой компанией, в соответствии с которым устанавливается получение физическим лицом определенных сумм начиная с условленного времени. Примером такого аннуитета может быть договор пенсионного страхования, когда с выходом на пенсию человеку начинают ежемесячно начисляться равные денежные суммы.
Формула расчета аннуитетных платежей
Рассчитать аннуитет довольно легко и это вполне можно сделать заранее, до заключения договора. Стоит произвести предварительный расчет ежемесячных выплат, общей их суммы к концу кредитования и сумму переплаты.
Величина ежемесячных платежей рассчитывается исходя из трех показателей:
- Сумма займа;
- Срок кредита;
- Коэффициента аннуитета.
Коэффициент аннуитета – это величина, которая позволяет рассчитать сумму ежемесячного платежа с учетом процентной ставки.
Для его расчета пользуются следующей формулой:
K = i * (1+i)n / ((1+i)n-1).
K – это коэффициент аннуитета,
i – процентная ставка за один расчетный период (например, месяц),
n – количество таких периодов.
Однако, здесь может пригодиться еще одна формула. Обычно заемщик знает величину годовой ставки, а для получения суммы ежемесячного платежа нужно знать ставку за расчетный период, то есть за месяц.
Для расчета этой величины нужна формула:
i = (1+r)1/12 – 1.
r в этой формуле – величина годовой ставки в сотых долях.
После расчета коэффициента аннуитета легко рассчитать сумму ежемесячного платежа, умножив коэффициент на всю сумму займа.
Формула расчета выглядит так:
P = K*S,
где P – размер ежемесячного взноса,
S – сумма кредита.
Общая сумма всех выплат (S1) вместе с процентами рассчитывается по формуле:
S1 = n*K*S.
То есть необходимо перемножить между собой количество расчетных периодов, коэффициент аннуитета и сумму кредита.
Для исчисления суммы переплаты (Ov) нужно из общей суммы всех выплат (S1) вычесть сумму кредита (S), то есть:
Ov = S1 – S.


Пример расчета аннуитетных платежей по кредиту
Для лучшего понимания формул можно взять пример ипотечного кредита на 15 лет суммой 3 000 000 р. с процентной ставкой 8% годовых и ежемесячными платежами.
Чтобы рассчитать коэффициент аннуитета нужно перевести количество лет в месяцы и вычислить ежемесячную процентную ставку (i).
15 лет – это 180 месяцев (15*12=180),
т. е. это срок кредита для расчета, n.
i = (1+0,08)1/12 – 1 = 0,0064.
Коэффициент аннуитета:
K = 0,0064*(1+0,064)180/((1+0,064)180-1) = 0,0093.
Величина ежемесячных платежей:
P = 0,0093*3 000 000 = 28 118,12.
Общая сумма кредита составит:
S1 = 180*0,0093*3 000 000 = 5 022 000.
Переплата при таком кредите будет равна:
Ov = 5 022 000-3 000 000 = 2 022 000.
Способы автоматизации аннуитетных расчетов
Производить такие расчеты вручную может показаться занятием утомительным. Поэтому возникает естественное желание автоматизировать процесс.
Сделать это можно двумя способами:
- Использовать формулу в табличном процессоре Exel;
- Воспользоваться кредитным калькулятором.
Ассортимент калькуляторов для расчета платежей в интернете велик, поэтому можно выбрать любой понравившийся. Это удобные программы, которые помимо суммы ежемесячных взносов могут рассчитать общую сумму переплаты, учесть в расчете различные комиссии, отобразить график платежей на протяжении всего периода кредитования.
Поэтому такой метод автоматизации аннуитетных расчетов наиболее простой и эффективный.
Но при желании или по необходимости можно воспользоваться и Excel. Для подобных расчетов в этой программе есть специальная функция ПЛТ (в английском интерфейсе PMT).
Она содержит 3 основных параметра:
- ставка (rate) – процентная ставка кредита,
- кпер (nper) – период кредитования;
- пс (pv) – общая сумма займа.
Так как задача – узнать сумму ежемесячных выплат, указывать все значения нужно в расчете на месяц. В соответствии с примером выше формула будет выглядеть следующим образом: = ПЛТ(8%/12;15*12;3000000). После ввода получаем сумму -28 669,56.
Стоит обратить внимание, что Excel чаще всего несколько округляет расчеты и они становятся более приближенными к реальным суммам выплат, т.к. в банках также принято округлять суммы. В связи с этим самостоятельные расчеты могут немного отличаться от полученных с помощью формулы.
Виды досрочного погашения при аннуитете

 Вопрос о том, как можно сократить срок выплаты кредита – итоговый, после разбора основных терминов, связанных с услугами кредитования, изучения особенностей разных типов этих услуг и расчета конкретных сумм, связанных с оплатой займа.
Вопрос о том, как можно сократить срок выплаты кредита – итоговый, после разбора основных терминов, связанных с услугами кредитования, изучения особенностей разных типов этих услуг и расчета конкретных сумм, связанных с оплатой займа.
Банки предлагают два варианта такого досрочного погашения кредита:
- сокращение срока кредитования;
- сокращение ежемесячной платы.
В первом случае сумма досрочного погашения должна быть не меньше суммы ежемесячного платежа. Во втором – в зависимости от размера взноса будет пересчитан график выплат.
Для осуществления процедуры досрочного погашения необходимо:
- Предоставить заявление о желании осуществить досрочный платеж.
- Внести необходимую сумму на счет.
- Получить подтверждение прохождения операции и новый график гашения кредита.
Важно учесть тот момент, что для банка ни один из этих вариантов невыгоден, соответственно существует много подводных камней, препятствующих досрочному погашению займа.
Основные возможные преграды для осуществления этой процедуры следующие:
- Запрет на полное или частичное досрочное погашение. В договорах редко запрещается оба варианта, но сама практика существует.
- Взимание дополнительной комиссии при досрочном погашении.
На сайтах многих банков можно воспользоваться услугой расчета досрочного погашения с помощью онлайн-калькулятора. Там же можно подробно изучить процедуру, которая в каждом банке имеет свои особенности.
Типы погашения кредита
Тип погашения кредита – значительный критерий при принятии решения воспользоваться услугами кредитования. Именно он определяет способ расчета стоимости кредита и суть процесса его погашения.
Существует два таких типа:
- Дифференцированный, при котором сумма взноса за период каждый раз меняется, так как заемщик выплачивает основную сумму долга плюс проценты на остаток займа. При этом тело кредита делится на равные доли на весь период кредитования, а проценты каждый раз снижаются.
- Аннуитетный – тип погашения кредита, подразумевающий выплату одинаковой фиксированной суммы каждый установленный период (месяц). В этом случае, несмотря на кажущуюся простоту расчета кредитного взноса, стоит учитывать неравномерность распределения этой суммы между телом займа и процентами.
Основное различие между этими типами состоит в последовательности погашения основного тела кредита и разницей сумм регулярных выплат. При дифференцированных платежах заемщик в первую половину срока кредитования выплачивает в основном тело кредита, а в аннуитетных – проценты.
При этом первый тип погашения кредита подразумевает взнос крупных сумм вначале и существенное их снижение к концу периода кредитования. А второй – внесение всегда равных сум на всем протяжении займа.
При выборе типа погашения кредита следует ориентироваться по таким параметрам:
- Уровень доходов. Если бюджет семьи невысок и нет возможности вносить разом крупные суммы, наилучшим выбором станут аннуитетные платежи. В этом случае человек имеет возможность взять в кредит крупную сумму на приемлемый срок без необходимости брать вначале невыполнимые обязательства по выплатам, а погашать кредит небольшими равными долями в течение всего срока кредитования.
- Возможность досрочного погашения кредита. Если вероятность появления такой возможности высока и, скорее всего, на середине срока кредитования заемщик решит внести всю оставшуюся сумму долга, то лучше выбрать дифференцированную систему платежей.
- Финансовая стабильность. При неустойчивом экономическом положении долгосрочный кредит лучше брать по дифференцированной системе, так как сумма выплат со временем будет уменьшаться. Но при кредитовании на короткие сроки и в случае, если человек уверен в своей финансовой устойчивости, лучшим выходом станет аннуитет.
Дифференцированный платеж
Итак, в некоторых случаях кредитование на условиях дифференцированного платежа может стать более подходящим.
Но тут есть свои особенности:
- Большую часть кредита (приблизительно две трети) необходимо будет погасить в первую половину срока кредитования. А это значит, что на первых порах такой займ станет довольно обременительным для бюджета.
- Общая сумма переплаты окажется ниже, чем при аннуитетных платежах, а суммы выплат будут постепенно снижаться, так как проценты начисляются при таком типе кредитования лишь на невыплаченную часть займа.
- Такой тип кредитования получить значительно сложнее, в связи с тем, что банк должен быть полностью уверен в платежеспособности клиента в первую часть периода договора.
Эти особенности обуславливают плюсы и минусы дифференцированных платежей.
В качестве достоинств можно отметить лишь два момента:
- Хорошие условия досрочного погашения.
- Менее обременительная система начисления процентов.
Недостатки такой системы следующие:
- Сравнительно непростая процедура получения такого кредита.
- Высокие размеры выплат в первую половину срока кредитования.
- Необходимость каждый установленный для взносов период уточнять сумму выплаты, что является причиной риска просрочить платеж из-за невнимательности заемщика или случайной ошибки сотрудника банка (в случае если последний назовет ошибочную сумму следующего взноса).


Принятие решения о взятии кредита требует ответственного и взвешенного подхода и прогнозирования всех возможных вариантов развития финансовой ситуации. Безусловно, аннуитетные платежи – удобная система при совершении крупных покупок или оплате долговременных и дорогостоящих услуг, но всегда нужно помнить о ее особенностях и осознанно подходить к принятию на себя таких кредитных обязательств.
Калькулятор аннуитетных платежей — расчет аннуитетных платежей по кредиту
В этой статье мы не станем сравнивать аннуитетный и дифференцированный тип кредитования, тем более этому посвящена отдельная статья. О выплате кредита по системе дифференцированных платежей слышали все, свою популярность она набирала многие годы, а с понятием аннуитетный кредит столкнулись совсем недавно. Прежде, чем углубляться в кредитные дебри, мы скажем сразу, Вы ничего не потеряете, кроме 3-5 минут на финансовую грамотность. Для конструктивного описания о том, как рассчитывать выплаты по такому займу и учиться использовать аннуитетный калькулятор, разберёмся, что это вообще такое.
Аннуитет предполагает погашение задолженности по кредиту платежами равного размера. Суть в том, что часть суммы, с помощью которой гасится основной кредитный взнос поэтапно увеличивается, а доля, которую выделяют на проценты наоборот уменьшается. Здесь мы когда-то добавим график, как это выглядит, но пока представьте это в своей голове.
Проведём параллель: в случае с дифференцированным кредитом, процент зависит от остатка по займу. В силу этого ежемесячный платёж постоянно уменьшается. Однако это не значит, что аннуитетный кредитный график менее выгодный. Просто он не всем подходит, но об этом позже.
Как рассчитать аннуитетный платёж с помощью кредитного калькулятора?
Мы старались сделать интерфейс максимально понятным, но если Вы считаете, что какие-то действия мы могли упростить, напишите об этом нам в социальных сетях. Для расчёта аннуитетного платежа по кредиту, изначально Вам потребуются всего 3 значения: сумма кредита, процент по кредиту и срок кредитования. На основании этих данных, Вы уже сможете сформировать график ежемесячных платежей на нашем сайте. Это можно сделать в расширенной версии заполнив только эти поля, либо в простой версии калькулятора на главной странице.

Мы по умолчанию ставим аннуитетный тип кредитования, так как на 2018-2019 год это самый выгодный вид кредита для банка, а так же для заёмщика с учетом его финансовых возможностей. Почему так? Об этом читайте дальше.
Если Вы всё же остановились на расширенной версии кредитного калькулятора, то легко сможете добавить единоразовую и ежемесячную комиссию. Под единоразовыми комиссиями мы подразумеваем обязательное страхование жизни, которое скорее всего Вас заставят приобрести при получении выгодных условий по кредиту, а под ежемесячными комиссиями мы считаем различного рода мусор, на который нельзя реагировать адекватно (пока его не уберут), к примеру: “комиссия за ведения счёта”, “комиссия за досрочное погашение”.

Кстати, мы отобрали около 130 банков для нашего сайта, и нашли много уловок, которыми пользуется банк. Но, всё же мы мечтатели и ищем идеальный банк для постоянных рекомендаций и вознесения в топ. Если Ваш банк именно такой, сообщите нам об этом в группе ВК. Мы всё еще независимая площадка в ру-нете и хотим донести эту информацию для всех.
Если Вы планируете частичное досрочное погашение, мы предусмотрели и этот вариант. Нажимая на дополнительный тумблер, Вы можете ввести любую сумму единоразово, либо выбрать периодичность платежа.

Выбор изменяемой процентной ставки так же доступен и находится под основным полем ввода процента по кредиту. Элементарные действия помогут изменить процентную ставку по кредиту в нужный период.

Занимательный факт, изменяемая процентная ставка в реалиях нашей страны всегда являлась мифом, но это не так. Она была всегда, особенно тогда, когда Вы переставали платить по кредиту какой-то период. Некоторые банки используют её во благо, мотивируя заёмщика платить меньше со второго или третьего года кредита, а некоторые банки пишут красивую процентную ставку на рекламных буклетах, к примеру, 10,9% годовых. По факту эта ставка станет актуальной только со второго года выплат по кредиту, где первый год Вас обяжут платить бешенные 34%.
Производя расчёт аннуитетного кредита с помощью кредитного калькулятора, Вы сможете сохранить график платежей, отправить его на электронную почту и после уже сравнить с графиком, представленным в банке. В своих расчётах мы используем официальные алгоритмы представленные Центральным Банком Российской Федерации. Если Вы нашли ошибку, сообщите нам об этом, мы обязательно ответим и устраним недочет в ближайшее время.
Самостоятельный расчёт аннуитетного платежа
Самый первый из вариантов – произвести расчёт аннуитетных платежей по кредиту на калькуляторе. Тем не менее, разбираться в тонкостях финансовых операций, проводящихся через банк, стоит уметь и самостоятельно. Специалисты банковского дела считают размер аннуитетных ставок по специальной формуле. В результате происходит составление графика, в котором расписывается порядок погашения аннуитета. Формула эта выглядит следующим образом:
Y = Sx(T+(T/(1+T)B-1))
Расшифруем указанные значения:
Y – сумма ежемесячного платежа;
T – процентная ставка;
B – время, на которое взят кредит в месяцах.
Чтобы рассчитать процент по аннуитетному платежу, необходимо остаток по займу умножить на годовой процент, а после разделить результат на 12 (количество месяцев в году). Выглядит это следующим образом:
Tn = SnxT/12
В этом случае:
Tn – начисленные проценты;
Sn – остаток;
T – годовая ставка по проценту.
Чтобы просчитать долю месячного платежа, использующуюся, как сумма погашения основной задолженности (самой суммы кредита, не процентов) в аннуитетной системе, следует от общего займа вычесть проценты:
S = Y-Tn
Здесь Y – это регулярный платёж;
Tn – процент, начисленный к моменту определённого (то есть n-ого) платежа.
Конечно, куда проще использовать специальный онлайн калькулятор аннуитетных платежей по кредиту, чем подсчитывать всё самостоятельно. Однако если вы желаете убедиться в честности банка, стоит научиться рассчитывать аннуитетный платёж самостоятельно. Ещё более рациональным решением будет использовать и аннуитетный калькулятор на нашем сайте.
Расчёт аннуитетного платежа в Excel
Калькуляторы не единственный способ автоматизированного расчета. На любом персональном компьютере есть табличные процессоры со встроенными функциями, подходящими для этой сложной операции. Например, в хорошо знакомой таблице Excel есть функция ПЛТ. С её помощью аннуитетная ставка рассчитывается следующим образом:
- Создаём чистый лист и в любой свободной ячейке задаём соответствующую функцию;
- Вводим необходимые параметры (которые запрашивает программа)
Когда вы закончите ввод, в ячейке увидите интересующую цифру. Простой метод, но не совсем объективный. Ведь есть много нюансов, о которых Excel совсем не спрашивает. Используйте этот метод, если Вы привыкли к данной программе или Вам захотелось испытать “новые возможности”, но в любом-другом случае откажитесь от этого способа.
Плюсы и минусы аннуитетного кредита
Ещё в начале статьи можно сделать вывод, что аннуитетные выплаты подходят не всем. Дело даже не в сложных расчётах,ведь калькуляторы аннуитетных платежей по кредиту, работающие в “онлайне”, решают эту проблему. Поэтому стоит очертить круг из тех, кому такой заём окажется выгодным.
Преимущества
| Недостатки
|
Говоря о фактах, кредит, на который действует аннуитетная схема выплат, несколько дороже. В банке Вам всегда посчитают именно аннуитетную ставку, так как она в большей степени выгодна банку. Единственная выгода для заёмщика – это сумма ежемесячного платежа аннуитета, которая значительно ниже до определенного момента.
У нас есть хорошая статья на тему сравнения аннуитетного и дифференцированного кредита с конкретными примерами, включая реальные факты из нашей жизни связанной с кредитами. Если у Вас есть ещё 5 минут на финансовую грамотность, обязательно прочитайте эту статью.
Досрочное погашение аннуитетного кредита
Всего есть два вариант досрочных выплат. Аннуитетный калькулятор рассчитан и на такие варианты погашения, поэтому достаточно просто знать, по каким сценариям могут развиваться события при необходимости отдать займ раньше срока. В банковском отделении Вам предложат такие варианты:
- Сократить период выплат в аннуитетной системе. Так, понадобится совершить дополнительный платёж. При этом месячная ставка не возрастёт. Платёж будет представлять собой компенсацию банку в размере процентов, которые он не получит.
- Уменьшение ежемесячных выплат. В этом случае уменьшается аннуитетная ставка, но размер процента не меняется (допустимо только при условии сокращения выплат по основной задолженности).
Такая возможность погашения аннуитета есть не везде. Даже включая, наш кредитный калькулятор. Скоро мы обязательно внесем в него правки и добавим эту возможность. Поэтому, рекомендуем произвести расчёт аннуитетных платежей по кредиту на калькуляторе с каждым досрочным погашением, если Вы всё же решили перейти к ежемесячному уменьшению выплат, а не к сокращению срока кредитования.
Коэффициент аннуитета Википедия
Аннуите́т (фр. annuité от лат. annuus — годовой, ежегодный) или финансовая рента — график погашения финансового инструмента, предполагающий выплату как основного долга, так и вознаграждения за пользование данным финансовым инструментом. Выплаты по аннуитету осуществляются равными суммами через равные промежутки времени. Сумма аннуитетного платежа включает в себя и основной долг, и вознаграждение.
Аннуитетом в широком смысле может называться:
- Один из видов срочного государственного займа, по которому ежегодно выплачиваются проценты и погашается часть суммы.
- Равные друг другу денежные платежи, выплачиваемые через определённые промежутки времени в счёт погашения полученного кредита, займа и процентов по нему.
- В страховании жизни — договор со страховой компанией, по которому физическое лицо приобретает право на регулярное получение согласованных сумм, начиная с определённого времени, например, выхода на пенсию
- Современная стоимость серии регулярных страховых выплат, производимых с определенной периодичностью в течение срока, установленного договором страхования.
Аннуитетный график также может использоваться для того, чтобы накопить определённую сумму к заданному моменту времени. В таком случае на счёт или депозит, по которому начисляется вознаграждение, регулярно вносятся одинаковые суммы.
Виды аннуитетов[ | ]
По времени выплаты первого аннуитетного платежа различают:
- аннуитет постнумерандо — выплата осуществляется в конце первого периода,
- аннуитет пренумерандо — выплата осуществляется в начале первого периода.
Коэффициент аннуитета[ | ]
Коэффициент аннуитета превращает разовый платёж сегодня в платёжный ряд. С помощью данного коэффициента определяется величина периодических равных выплат по кредиту:
K=i⋅(1+i)n(1+i)n−1{\displaystyle K={\frac {i\cdot (1+i)^{n}}{(1+i)^{n}-1}}},
где i{\displaystyle i} — процентная ставка за один период, n{\displaystyle n} — количество периодов на протяжении всего действия аннуитета (количество операций по капитализации процентов). На практике возможны некоторые отличия от математического расчёта, вызванные округлением, а также неодинаковой продолжительностью месяца и года; особенно это касается последнего по сроку платежа.
Предполагается, что выплаты производятся постнумерандо, то есть в конце каждого периода. И тогда величина периодической выплаты A=K⋅S{\displaystyle A=K\cdot S}, где S{\displaystyle S} — величина кредита.
CFA — Как рассчитывать приведенную стоимость (PV) серии денежных потоков (аннуитета и перпетуитета)? | программа CFA
Многие аспекты управления инвестициями часто связаны с активами, которые предполагают серию (т.е. последовательность) денежных потоков, возникающих с течением времени.
Денежные потоки могут быть очень неравномерными, относительно одинаковыми или равными.
Также денежные потоки могут возникать в течение относительно коротких периодов времени, более длительных периодов времени или даже растягиваться на неопределенный срок.
Далее мы обсудим, как найти текущую или приведенную стоимость (PV) серии денежных потоков.
Расчет текущей стоимости (PV) серии равных денежных потоков.
Начнем с обычного или простого аннуитета (англ. ‘ordinary annuity’). Напомним, что обычный аннуитет означает равные аннуитетные платежи, причем 1-й платеж начинается через 1 период (т.е. в конце текущего периода / начале следующего / при t = 1).
Всего простой аннуитет включает N платежей с первым взносом при t = 1 и последним при t = N.
Мы можем выразить текущую (приведенную) стоимость обычного аннуитета как совокупность текущей стоимости каждого отдельного аннуитетного платежа, как указано ниже:
\( \mathbf {PV = {A \over (1 + r)} + {A \over (1 + r) ^ 2} + {A \over (1 + r) ^ 3} + \cdots + {A \over (1 + r)^{N-1}} + {A \over (1 + r)^N}} \) (формула 10)
где:
- A = сумма аннуитета,
- r = процентная ставка за период, соответствующая частоте выплаты аннуитета (например, годовой, ежеквартальный или ежемесячный),
- N = количество аннуитетных платежей.
Поскольку аннуитетный платеж (A) является константой в этом уравнении, его можно вывести за скобки. Таким образом, это выражение можно привести к следующей формуле:
\( \mathbf {PV = A \left [1- {1 \over (1 + r)^N} \over r \right]} \) (формула 11)
Точно так же, как и при вычислении будущей стоимости (FV) обычного аннуитета, мы находим текущую стоимость (PV), умножая сумму аннуитета на фактор текущей стоимости аннуитета (англ. ‘present value annuity factor’) — он заключен в квадратные скобки в формуле 11.
Пример расчета текущей (приведенной) стоимости обычного аннуитета.
Предположим, вы рассматриваете возможность покупки финансового актива, который обещает выплату в €1 000 каждый год в течение 5 лет с первым платежом через год.
Норма прибыли составляет 12% в год.
Сколько вы должны заплатить за этот актив?
Решение:
Чтобы узнать стоимость финансового актива, используйте формулу (11) текущей стоимости обычного аннуитета, со следующими данными:
A = €1,000
r = 12% = 0.12
N = 5
\( \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= €1 \ 000 \left[ 1-{1\over(1.12)^5} \over 0.12 \right] \end{aligned} } \)
= €1,000 * (3.604776)
= €3,604.78
Серия денежных потоков в размере €1,000 в год в течение 5 лет на текущую дату составляет €3,604.78 при дисконтировании по ставке 12%.
Необходимость отслеживания фактических календарных сроков приводит нас к специфическому типу аннуитета: авансовому аннуитету или аннуитету пренумерандо (англ. ‘annuity due’).
При авансовом аннуитете 1-ый платеж выполняется в текущую дату (t = 0). В общей сложности авансовый аннуитет включает N платежей.
На рисунке ниже представлена временная шкала авансового аннуитета из 4-х платежей в размере $100.
 Авансовый аннуитет в размере $100 за период.
Авансовый аннуитет в размере $100 за период.
На рисунке мы можем видеть авансовый аннуитет с 4-мя периодами, состоящий из двух частей:
- единовременная сумма в размере $100 на текущую дату (при t = 0) и
- обычный аннуитет в размере $100 за период в течение 3-х периодов.
При ставке дисконтирования в 12% четыре денежных потока в размере 100$ в этом примере авансового аннуитета будут стоить $340,18.
Существует альтернативный способ расчета текущей стоимости авансового аннуитета.
По сравнению с обычным аннуитетом каждый платеж авансового аннуитета дисконтируется на 1 период раньше.
Поэтому мы можем модифицировать формулу 11, умножив правую часть уравнения на (1 + r):
PV (Авансовый аннуитет) = \( \mathbf {A \left[ 1-(1+r)^{-N} \over r \right] (1+r) } \)
Выражение стоимости будущих денежных потоков в сегодняшнем эквиваленте дает нам удобный способ сравнения аннуитетов. Следующий пример иллюстрирует этот подход.
Пример расчета авансового аннуитета как суммы текущей стоимости единичного денежного потока и обычного аннуитета.
Вы выходите на пенсию сегодня и должны либо получить свое пенсионное пособие в виде паушальной суммы (т.е. единовременной выплаты всех пенсионных накоплений), либо в виде аннуитета.
Сотрудник вашей компании, занимающийся выплатой пособий, предлагает вам две альтернативы:
- немедленную единовременную выплату в размере $2 млн. или
- аннуитет с 20 платежами в размере $200 000 в год с первым платежом от текущей даты.
Процентная ставка в вашем банке составляет 7% годовых с ежегодным начислением процентов.
Какой вариант обеспечивает большую текущую стоимость? (Игнорируйте любые налоговые различия между двумя вариантами.)
Решение:
Чтобы сравнить эти два варианта, необходимо найти текущую стоимость каждого из них в момент времени
t = 0 и выбрать наибольшее значение.
Текущая стоимость первого варианта составляет $2 млн., т.е. первый вариант уже выражен в сегодняшнем эквиваленте.
Второй вариант — аннуитет. Поскольку первый платеж происходит при t = 0, вы можете разделить этот аннуитет на две части:
- немедленную выплату $200 000 от текущей даты (t = 0) и
- обычный аннуитет в размере $200 000 в год в течение 19 лет.
Чтобы рассчитать этот аннуитет, вам нужно найти текущую стоимость обычного аннуитета, используя формулу 11, а затем добавить к нему 200 000 долларов.
A = $200,000
N = 19
r = 7% = 0.07
\( \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= $200\ 000 \left[ 1-{1\over(1.07)^{19}} \over 0.07 \right] \end{aligned} } \)
= $200,000(0.335595)
= $2,067,119.05
19 платежей в размере $200 000 имеют текущую (приведенную) стоимость в размере $2,067,119.05. Добавив к этой сумме первоначальный платеж в размере $200,000, мы обнаружим, что общая стоимость аннуитета составляет $2,267,119.05.
Текущая стоимость аннуитета больше, чем единовременная альтернатива в размере $2 млн.
Теперь рассмотрим другой пример, подтверждающий эквивалентность текущей и будущей стоимости.
Пример расчета прогнозируемой текущей стоимости обычного аннуитета.
Менеджер немецкого пенсионного фонда ожидает, что пенсионерам будут выплачиваться пособия в размере €1 млн. в год. Пенсионные выплаты начнут осуществляться через 10 лет от текущей даты, при t = 10.
После того, как пособия начнут выплачиваться, эти выплаты продлятся до t = 39, что составляет в общей сложности 30 платежей.
Какова текущая (приведенная) стоимость пенсионного обязательства, если соответствующая годовая ставка дисконтирования для обязательств по пенсионному плану составляет 5% годовых, начисляемых ежегодно?
Решение:
Эта задача связана с аннуитетом, первый платеж по которому наступает через 10 лет, при t = 10.
При этом, на момент t = 9 мы имеем обычный аннуитет с 30 платежами. Мы можем вычислить текущую стоимость (PV) этого аннуитета с помощью формулы 11, а затем посмотреть на нее на временной шкале.
A = €1,000,000
r = 5% = 0.05
N = 30
\( \mathbf { \begin{aligned} PV &= A \left[ 1-{1\over(1+r)^N} \over r \right] \\ &= €1 \ 000 \ 000 \left[ 1-{1\over(1.05)^{30}} \over 0.05 \right] \end{aligned} } \)
= €1,000,000 * (15.372451)
= €15,372,451.03
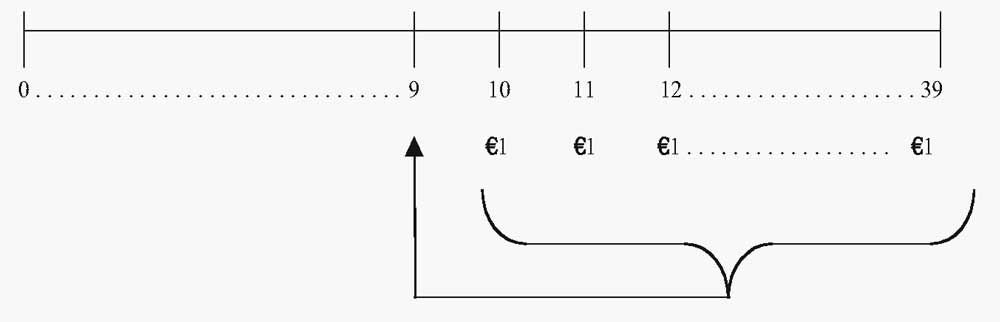 Текущая стоимость обычного аннуитета с первым платежом в момент времени t = 10 (в млн. €).
Текущая стоимость обычного аннуитета с первым платежом в момент времени t = 10 (в млн. €).
На временной шкале мы отразили пенсионные выплаты в размере €1 млн., занимающие отрезок от t = 10 до t = 39.
Фигурная скобка и стрелка обозначают процесс нахождения текущей стоимости аннуитета, дисконтированной к моменту времени t = 9.
Текущая стоимость (PV) пенсионных пособий по состоянию на t = 9 составляет €15,372,451.03.
Далее задача заключается в том, чтобы найти текущую стоимость на текущую дату (при t = 0). Теперь мы можем полагаться на эквивалентность текущей стоимости и будущей стоимости (см. CFA — Эквивалентность приведенной и будущей стоимости денежных потоков).
Как показано на временной лини, мы можем рассматривать сумму при t = 9 в качестве будущей стоимости с точки зрения t = 0.
Мы вычислим текущую стоимость (PV) при t = 0 следующим образом:
FVN = €15,372,451.03 (текущая стоимость при t = 9)
N = 9
r = 5% = 0.05
PV = FVN * (1 + r)—N
= €15,372,451.03 * (1.05)-9
= €15,372,451.03 * (0.644609)
= €9,909,219.00
Приведенная стоимость на текущую дату (при t = 0) пенсионного обязательства составляет €9,909,219.00.
Приведенный пример иллюстрирует три процедуры:
Как вычислять текущую стоимость (PV) бесконечной серии равных денежных потоков — бессрочный аннуитет?
Рассмотрим случай обычного аннуитета, который продолжается бесконечно. Такой обычный аннуитет называется бессрочным аннуитетом или перпетуитетом или вечной рентой (англ. ‘perpetuity’ или ‘perpetual annuity’).
Чтобы получить формулу для текущей стоимости перпетуитета, мы можем модифицировать формулу 10, чтобы учесть бесконечную последовательность денежных потоков:
\( \mathbf {PV = A \sum _{t = 1} ^{\infty} \left[ 1 \over (1 + r)^t \right] } \) (формула 12)
Пока процентные ставки положительны, сумма факторов текущей стоимости позволяет получить формулу в следующем виде:
PV = A / r (формула 13)
Чтобы понять смысл этого преобразования, обратите внимание на формулу (11) текущей стоимости обычного аннуитета.
Поскольку N (количество периодов в аннуитете) переходит на бесконечность, выражение 1 / (1 + r)N приближается к 0, а формула 11 упрощается до формулы 13.
Эта формула потребуется, когда мы будем оценивать дивиденды от акций, поскольку акции не имеют предопределенного срока действия.
Акция, выплачивающая постоянные дивиденды, аналогична бессрочному аннуитету.
При первом платеже через год от текущей даты, перпетуитет в размере $10 в год при 20%-ой норме прибыли имеет текущую стоимость в размере $10 / 0,2 = $50 долларов.
Формула 13 справедлива только для бессрочного аннуитета с равными платежами. В примере выше первый платеж произошел при t = 1; поэтому мы вычисляем текущую стоимость при t = 0.
Некоторые финансовые активы также соответствуют концепции бессрочного аннуитета. Определенные государственные облигации и привилегированные акции являются типичными примерами финансовых активов, которые обеспечивают равные выплаты в течение неопределенного срока.
Пример расчета текущей стоимости (PV) перпетуитета.
Британское правительство когда-то выпускало форму ценных бумаг, называемых «консолями» (англ. ‘consol bond’). Это — бессрочные облигации (англ. ‘perpetual bond’), которые обеспечивают равные денежные выплаты в течение неограниченного срока.
Если бессрочная облигация приносит £100 в год в течение неограниченного срока, сколько бы она стоила сегодня, если норма прибыли составляет 5%?
Решение:
Чтобы ответить на этот вопрос, мы можем использовать формулу 13 со следующими данными:
A = £100
r = 5% = 0.05
PV = A/r
= £100/0.05
= £2,000
Облигация будет стоить £2 000.
Текущая стоимость на момент времени, отличный от текущей даты (t = 0).
На практике финансовым аналитикам часто приходится находить текущие значения стоимости, на различные моменты времени, отличные от t = 0.
Если мы рассчитаем перпетуитет, начинающийся с платежа в размере $100 на 2-й год, то мы получим PV1 = $ 100 / 0,05 = $2 000 при 5%-й ставке. Кроме того, мы можем рассчитать PV на текущую дату как PV0 = $2,000 / 1.05 = $ 1,904.76.
Рассмотрим аналогичную ситуацию, в которой денежные потоки в размере $6 в год начинаются в конце 4-го года и продолжаются в конце каждого года после этого с последним потоком денежных средств в конце 10-го года.
По состоянию на конец 3-го года мы сталкиваемся с типичным 7-летним обычным аннуитетом. Мы можем найти текущую стоимость аннуитета на конец 3-го года, а затем привести эту стоимость к текущей дате.
При процентной ставке 5% денежные потоки в размере $6 в год, начинающиеся в конце 4-го года, будут стоить $34,72 на конец 3-го года (t = 3) и $29,99 на текущую дату (t = 0).
Следующий пример иллюстрирует важную концепцию, согласно которой начинающийся в будущем аннуитет или перпетуитет может быть выражен в текущей стоимости за один период до первого платежа. Эта стоимость может быть приведена к текущей стоимости на сегодняшнюю дату.
Пример расчета текущей стоимости (PV) бессрочного аннуитета (перпетуитета) с отсроченной первой выплатой.
Рассмотрим перпетуитет с равными платежами в £100 в год, с первой выплатой, начинающейся при t = 5.
Какова будет его текущая стоимость на сегодняшнюю дату (при t = 0), при 5-процентной ставке дисконтирования?
Решение:
Во-первых, мы находим текущую стоимость перпетуитета при t = 4, а затем дисконтируем эту сумму к текущей дате t = 0. (Напомним, что у перпетуитета и обычного аннуитета первый платеж осуществляется на конец первого периода, что объясняет индекс t = 4 для нашего расчета текущей стоимости).
1. Находим текущую стоимость перпетуитета при t = 4:
A = £100
r = 5% = 0.05
PV = A/r
= £100/0.05
= £2,000
2. Находим текущую стоимость будущего значения при
t = 4.
С точки зрения сегодняшней даты t = 0 текущую стоимость в £2,000 можно считать будущей стоимостью.
Теперь нам нужно найти текущую стоимость £2,000 при
t = 0:
FVN = £2,000 (текущая стоимость при t = 4)
r = 5% = 0.05
N = 4
PV = FVN * (1 + r)—N
= £2,000 * (1.05)-4
= £2,000 * (0.822702)
= £1,645.40
Приведенная стоимость перпетуитета на текущую дату составляет £1,645.40.
Как обсуждалось ранее, аннуитет представляет собой серию платежей с фиксированной (одинаковой) суммой в течение определенного количества периодов.
В ситуации с перпетуитетом число периодов бесконечно. В этом случае мы предоставляем бессрочное обязательство производить платежи, и эти платежи имеют одинаковую сумму. Тем не менее, первая (1) часть перпетуитета отсрочена и выплачивается при t = 5; после этого платежи продолжаются бесконечно.
Выплаты по второй (2) части перпетуитета компенсируют смещение 1-го платежа первой (1) части перпетуитета к t = 5.
Благодаря этому перпетуитет с отсроченной 1-й выплатой (до t = 5) обеспечивает выплаты при t = 1, 2, 3 и 4. Выплаты за эти 4 периода точно соответствуют определению обычного аннуитета с четырьмя платежами.
Таким образом, мы можем представить обычный аннуитет как разницу между двумя перпетуитетами с равными платежами, но с разными датами начала выплат.
Следующий пример иллюстрирует этот результат.
Пример расчета текущей стоимости обычного аннуитета как разницы между текущей стоимостью (PV) и прогнозируемым (отсроченным) перпетуитетом.
С учетом 5%-ой ставки дисконтирования, найдите текущую (приведенную) стоимость 4-летнего обычного аннуитета в размере £100 в год, с выплатами начиная с 1-го года, в качестве разницы между следующими двумя перпетуитетами:
- Перпетуитет 1 на £100 в год, начиная с 1-го года (первый платеж при t = 1).
- Перпетуитет 2 на £100 в год, начиная с 5-го года (первый платеж при t = 5).
Решение:
Если мы вычтем Перпетуитет 2 из Перпетуитета 1, мы получим обычный аннуитет в размере £100 за 4 года (платежи при t = 1, 2, 3, 4).
Вычитая текущую стоимость Перпетуитета 2 из Перпетуитета 1, мы придем к текущей (приведенной) стоимости четырехлетнего обычного аннуитета:
PV0 (Перпетуитет 1) = £100 / 0.05 = £2,000
PV4 (Перпетуитет 2) = £100 / 0.05 = £2,000
PV0 (Перпетуитет 2) = £2,000 / (1.05)4 = £1,645.40
PV0 (Аннуитет)
= PV0 (Перпетуитет 1) — PV0 (Перпетуитет 2)
= £2,000 — £1,645.40
= £354.60
Текущая стоимость 4-летнего обычного аннуитета равна £2,000 — £1,645.40 = £354.60.
Как вычислять текущую стоимость (PV) для серии неравных денежных потоков?
Когда мы имеем неравные денежные потоки, мы должны сначала найти текущую стоимость (PV) каждого отдельного денежного потока, а затем суммировать соответствующие значения PV.
Для серии (последовательности) с большим количеством денежных потоков мы обычно используем электронную таблицу.
В таблице ниже приведена последовательность денежных потоков с
- временными периодами в 1-м столбце,
- денежными потоками во 2-м столбце и
- текущей стоимостью (PV) каждого денежного потока в 3-м столбце.
В итоговой строке таблице показана сумма приведенных значений для всей серии денежных потоков.
|
Период
|
Денежный поток ($)
|
PV при t=0
| |
|---|---|---|---|
|
1
|
1,000
|
$1,000(1.05)-1 =
|
$952.38
|
|
2
|
2,000
|
$2,000(1.05)-2 =
|
$1,814.06
|
|
3
|
4,000
|
$4,000(1.05)-3 =
|
$3,455.35
|
|
4
|
5,000
|
$5,000(1.05)-4 =
|
$4,113.51
|
|
5
|
6,000
|
$6,000(1.05)-5 =
|
$4,701.16
|
|
|
|
Сумма =
|
$15,036.46
|
Мы могли бы рассчитать будущую стоимость (FV) серии этих денежных потоков, вычислив ее по отдельности для каждого потока с использованием формулы расчета будущей стоимости.
Однако мы уже знаем текущую стоимость этой серии, поэтому мы можем легко применить принцип временной эквивалентности для всей суммы денежных потоков сразу.
Будущая стоимость серии денежных потоков составляет $19,190.76 и эквивалентна единовременному денежному потоку размере $15,036.46, с приведением к периоду t = 5:
PV = $15,036.46
N = 5
r = 5% = 0.05
FVN = PV * (1 + r)N
= $15,036.46 * (1.05)5
= $15,036.46 * (1.276282)
= $19,190.76
Аннуитеты в МСФО
В данной статье мы продолжим говорить о дисконтировании денежных потоков и в этот раз речь пойдет об аннуитетных денежных потоках.
Что такое аннуитет?
Аннуитет – это серия одинаковых платежей через одинаковые промежутки времени. Это могут быть ежегодные, ежеквартальные, ежемесячные платежи. Например, фиксированная сумма зарплата, арендных выплат, платежей банку по кредиту и т.д.
Аннуитеты бывают пренумерандо и постнумерандо. Данные термины обозначают момент платежа. Термин пренумерандоозначает платежи в начале каждого периода, постнумерандо — в конце временного периода.
Формула аннуитета
Аннуитетные денежные потоки также можно дисконтировать, то есть определять их текущую стоимость. Например, это необходимо, когда нам нужно выбрать между двумя предлагаемых нам вариантами получения денег.
Дисконтирование аннуитетных платежей
ПРИМЕР 1. Необходимо выбрать наиболее выгодный вариант:
А) получить 40,000 долларов сегодня или
(Б) 5 раз по 10,000 долларов в конце каждого из следующих 5 лет.
Банковская ставка для получения кредита на данный срок составляет 10%.
На первый взгляд вариант (Б) в сумме лучше (5 х 10,000 = 50,000), чем 40,000 долларов. Но действительно ли это так? Ведь мы знаем, что у денег есть еще и «временная» стоимость. Чтобы сравнить эти два варианта между собой, надо привести их к одному моменту времени (к моменту «сейчас»), поскольку стоимость денег в разные моменты времени различна. В данном случае надо продисконтировать аннутитетный денежный поток (Б), т.е. рассчитать его сегодняшнюю стоимость.
Для начала давайте вспомним, как выглядит формула дисконтирования:
PV = FV х 1/(1+R)n
где,
Future value (FV) – будущая стоимость Present value (PV) – текущая (дисконтированная/приведенная) стоимость. R – ставка процента (норма доходности, требуемая инвестором), N – число лет от даты в будущем до текущего момента
Коэффициенты дисконтирования, используемые для нашего примера 1/(1+R)n — это 0.9091, 0.8264 и т.д. Только эти вычисления придется повторить 5 раз и сложить. Если продисконтировать (то есть привести к текущему моменту) каждую сумму отдельно, то получится вот такая таблица:
10,000 х 0,9091 = 9,091
10,000 х 0,8264 = 8,264
10,000 х 0,7513 = 7,513
10,000 х 0,6830 = 6,830
10,000 х 0,6209 = 6,209
Итого: 37,907
Здесь сумма платежа умножена на соответствующий каждому году коэффициент дисконтирования. В итоге, пять платежей по 10,000 долларов в конце каждого года с учетом дисконтирования стоят 37,907 долларов, что немного меньше, чем 40,000 сегодня. Следовательно, при ставке 10%, 40,000 долларов сегодня будет выгоднее, чем предложенный аннуитет 5 лет по 10,000 долларов.
Формулу дисконтированной стоимости аннуитета можно записать следующим образом:
PV = PMT х [1/(1+R)1 + 1/(1+R)2 + 1/(1+R)3 + 1/(1+R)4 +1/(1+R)5] = 10,000 х (0.9091+0.8264+0.7513+0.6830+0.6209) = 10,000 х 3.7907 = 37,907
где PMT (от английского payment) – это сумма аннуитетного платежа.
Как Вы могли заметить, вместо того чтобы дисконтировать каждую сумму отдельно, можно сложить все коэффициенты дисконтирования и умножить только один раз. Результат сложения коэффициентов дисконтирования за 5 лет называется коэффициентом аннуитета. В данном примере коэффициент аннуитета равен 3,7907.
Таким образом, для нахождения текущей стоимости аннуитетов необходимо разовый платеж умножить на коэффициент аннуитета (10,000*3,7907 = 37,907).
Итак, мы разобрали пример с аннуитетными платежами в конце каждого года (постнумерандо) .
ПРИМЕР 2. Давайте немного изменим условия нашего примера. Необходимо выбрать наиболее выгодный вариант:
А) получить 40,000 долларов сегодня или
Б) 5 раз по 10,000 долларов в начале каждого из следующих 5 лет.
Это будет так называемый аннуитет пренумерандо.
В данной ситуации, так как первый платеж производится в начале года, то самый важный нюанс, о котором надо помнить, это то что, первый платеж не надо дисконтировать (т.е. приводить к настоящему моменту). Другими словами, для первого платежа используется коэффициент дисконтирования равный единице. Но необходимо дисконтировать остальные 4 платежа, так как они отложены во времени. Для иллюстрации составим следующую таблицу:
10,000 х 1.000 = 10,000
10,000 х 0.9091 = 9,091
10,000 х 0.8264 = 8,264
10,000 х 0.7513 = 7,513
10,000 х 0.6830 = 6,830
Итого: 41,698
Следовательно, предложенный аннуитет 5 лет по 10,000 в начале года будет выгоднее, чем 40,000 сегодня при ставке 10%.
Формула дисконтированной стоимости аннуитета:
PV = PMT + PMT х [1/(1+R)1 + 1/(1+R)2 + 1/(1+R)3 + 1/(1+R)4] = 10,000 + 10,000 х (0.9091+0.8264+0.7513+0.6830) = 10,000 + 10,000 х 3.1698 = 41,698
Обратите внимание, что в данном примере мы определили коэффициент аннуитета для четырех отложенных во времени платежей, а не для пяти, а первый платеж не дисконтировали.
Как видно из данных примеров, большое значение имеет момент, когда производятся платежи: в начале или в конце периода. Поэтому, если нужно рассчитать дисконтированную стоимость аннуитетных денежных потоков, желательно рисовать шкалу времени, на которой отметить суммы и коэффициенты, соответствующие каждому периоду.
Все блоги
Аннуитет — это… Что такое Аннуитет?
Аннуите́т (фр. annuité от лат. annuus — годовой, ежегодный) или финансовая рента — общий термин, описывающий график погашения финансового инструмента (выплаты вознаграждения или уплаты части основного долга и процентов по нему), когда выплаты устанавливаются периодически равными суммами через равные промежутки времени. Аннуитетный график отличается от такого графика погашения, при котором выплата всей причитающейся суммы происходит в конце срока действия инструмента, или графика, при котором на периодической основе выплачиваются только проценты, а вся сумма основного долга подлежит к оплате в конце.
Сумма аннуитетного платежа включает в себя основной долг и вознаграждение.
В широком смысле, аннуитетом может называться как сам финансовый инструмент, так и сумма периодического платежа, вид графика погашения финансового инструмента или другие производные понятия, оттенки значения. Аннуитетом, например, является:
- Один из видов срочного государственного займа, по которому ежегодно выплачиваются проценты, и погашается часть суммы.
- Равные друг другу денежные платежи, выплачиваемые через определённые промежутки времени в счёт погашения полученного кредита, займа и процентов по нему.
- Соглашение или контракт со страховой компанией, по которому физическое лицо приобретает право на регулярно поступающие суммы, начиная с определённого времени, например, выхода на пенсию.
- Современная стоимость серии регулярных выплат, производимых с определенной периодичностью в течение срока, установленного договором страхования.
Аннуитетный график также может использоваться для того, чтобы накопить определённую сумму к заданному моменту времени, внося равновеликие вклады на счёт или депозит, по которому начисляется вознаграждение.
Виды аннуитетов
По времени выплаты первого аннуитетного платежа различают:
- аннуитет постнумерандо — выплата осуществляется в конце первого периода,
- аннуитет пренумерандо — выплата осуществляется в начале первого периода.
Коэффициент аннуитета
Коэффициент аннуитета превращает разовый платёж сегодня в платёжный ряд. С помощью данного коэффициента определяется величина периодических равных выплат по кредиту:
где — процентная ставка за один период (всего периодов n), — количество периодов на протяжении всего действия аннуитета.
(следует учитывать, что данная формула является чисто математической, то есть на практике возможны некоторые девиации, вызванные округлением, а также неодинаковой продолжительностью месяца и года; особенно это касается последнего по сроку платежа).
Предполагается, что выплаты производятся постнумерандо, то есть в конце каждого периода. И тогда величина периодической выплаты A = K·S, где S — величина кредита.
Пример расчёта. Рассчитаем ежемесячную выплату по трехлетнему кредиту суммой $ 12000 по ставке 6 % годовых. Поскольку выплаты будут производиться каждый месяц, необходимо привести процентную ставку из годового значения к месячному: 6 %/12 = 0,5 %, или 0,005 в месяц. Подставляем в указанную выше формулу следующие значения: , мес. Полученный коэффициент умножаем на сумму кредита — 12000. Получаем 365 $/мес.
Обычно погашение долга предусматривает ежемесячные или ежеквартальные выплаты, и задаётся годовая процентная ставка . Если выплаты производятся постнумерандо раз в год в течение лет, то точная формула для коэффициента аннуитета:
или по упрощенной формуле:
где (всегда показатель степени) — количество периодов = n*m.
Будущая стоимость аннуитетных платежей
Будущая стоимость аннуитетных платежей предполагает, что платежи осуществляются на приносящий проценты вклад. Поэтому будущая стоимость аннуитетных платежей является функцией как величины аннуитетных платежей, так и ставки процента по вкладу.
Будущая стоимость серии аннуитетных платежей (FV) вычисляется по формуле (предполагается сложный процент)
- ,
где r — ставка процента, n — количество периодов, в которые осуществляются аннуитетные платежи, X — величина аннуитетного платежа.
Аннуитет пренумерандо в рассматриваемом случае начисления процентов по аннуитетным платежам, имеет на один год начисления процентов больше. Поэтому формула для вычисления будущей стоимости аннуитета пренумерандо приобретает следующий вид
В табличных процессорах в состав финансовых функций входит функция для вычисления будущей стоимости аннуитетных платежей. В OpenOffice.org Calc для вычисления будущей стоимости аннуитетных платежей (как постнумерандо, так и пренумерандо) применяется функция FV.
См. также
Ссылки
Аннуитетные платежи — расчёт, формула
Аннуитетный платеж — вариант ежемесячного платежа по кредиту, когда размер ежемесячного платежа остаётся постоянным на всём периоде кредитования.
Ежемесячный платёж, при аннуитетной схеме погашения кредита состоит из двух частей. Первая часть платежа идёт на погашение процентов за пользование кредитом. Вторая часть идёт на погашение долга. Аннуитетная схема погашения отличается от дифференцированной тем, что в начале кредитного периода проценты составляют большую часть платежа. Тем самым сумма основного долга уменьшается медленно, соответственно переплата процентов при такой схеме погашения кредита получается больше.
При аннуитетной схеме выплат по кредиту, ежемесячный платёж рассчитывается как сумма процентов, начисленных на текущий период и суммы идущей на погашения суммы кредита.
Для расчёта размера ежемесячного платежа можно воспользоваться кредитным калькулятором. С помощью калькулятора кредитов можно определить размер начисленных процентов, а так же сумму, идущую на погашение долга. Кроме того, можно взять в руки обычный калькулятор и рассчитать график платежей вручную.
Расчёт аннуитетного платежа
Рассчитать месячный аннуитетный платеж можно по следующей формуле:
, где x – месячный платёж, S – первоначальная сумма кредита, P – (1/12) процентной ставки, N – количество месяцев. |
Формула, для определение того, какая часть платежа пошла на погашение кредита, а какая на оплату процентов является достаточно сложной и без специальных математических знаний простому обывателю будет сложно ей воспользоваться. Поэтому мы рассчитаем данные величины простым способом, дающим такой же результат.
Для расчета процентной составляющей аннуитетного платежа, нужно остаток кредита на указанный период умножить на годовую процентную ставку и всё это поделить на 12 (количество месяцев в году).
| , где – начисленные проценты, — остаток задолженности на период, P – годовая процентная ставка по кредиту. |
Что бы определить часть, идущую на погашение долга, необходимо из месячного платежа вычесть начисленные проценты.
| s = x — , где s – часть выплаты, идущая на погашение долга, x – месячный платёж, — начисленные проценты, на момент n-ой выплаты. |
Поскольку часть, идущая на погашение основного долга зависит от предыдущих платежей, поэтому рассчёт графика, по данной методике вычислять последовательно, начиная с первого платежа.
Пример расчёта графика выплат по аннуитетному кредиту
Для примера рассчитаем график платежей по кредиту в размере 100000 р. и годовой процентной ставкой 10%. Сроком погашения кредита возьмём 6 месяцев.
Для начала рассчитаем ежемесячный платёж.
Затем рассчитаем по месяцам процентную и кредитную часть аннуитетного платежа.
| 1 месяц Проценты: 100000 * 0,1 / 12 = 833,33 Основной долг: 17156,14 – 833, 33 = 16322,81 2 месяц Остаток кредита: 100000 – 16322,81 = 83677,19 Проценты: 83677,19 * 0,1/12 = 697,31 Основной долг: 17156,14 – 697,31 = 16458,83 3 месяц Остаток кредита: 83677,19 — 16458,83 = 67218,36 Проценты: 67218,36 *0,1/12 = 560,15 Основной долг: 17156,14 – 560,15 = 16595,99 4 месяц Остаток кредита: 67218,36 — 16595,99 = 50622,38 Проценты: 50622.38 * 0,1/12 = 421.85 Основной долг: 17156,14 – 421,85 = 16734,29 5 месяц Остаток кредита: 50622,38 — 16734,29 = 33888,09 Проценты: 33888,09 * 0,1/12 = 282,40 Основной долг: 17156,14 – 282,40 = 16873,74 6 месяц Остаток кредита: 33888.09 — 16873.74 = 17014,35 Проценты: 17014,35 * 0,1/12 = 141,79 Основной долг: 17156,14 – 141,79 = 17014,35 |
Если интересно узнать размер переплаты по аннуитетному кредиту, необходимо ежемесячный платёж, умножить на количество периодов и из получившегося числа вычесть первоначальный размер кредита. В нашем случае переплата будет следующей:
| 17156,14 * 6 – 100000 = 2936,84 |
Результат подсчётов по нашему примеру на сайте www.platesh.ru будет выглядеть так:
Форма ввода данных для расчёта аннуитетного платежа
Пример графика аннуитетных платежей
Что подтверждает правильность наших расчётов.
